Случайную реализацию х(t) можно разложить по детерминированным ортогональным функциям  Коэффициенты такого разложения сn будут случайными величинами. Для гармонического разложения
Коэффициенты такого разложения сn будут случайными величинами. Для гармонического разложения 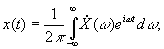
 Ввиду случайности спектральной плотности
Ввиду случайности спектральной плотности 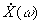 и равенства нулю ее среднего значения при усреднении по всем реализациям при
и равенства нулю ее среднего значения при усреднении по всем реализациям при  (ввиду случайности и независимости фаз спектральных составляющих в различных реализациях) она не используется для характеристики случайного процесса. Поэтому для случайного процесса x(t) вводится понятие спектральной плотности мощности, связанной с автокорреляционной функцией преобразованием Фурье (соотношение Винера - Хинчина).
(ввиду случайности и независимости фаз спектральных составляющих в различных реализациях) она не используется для характеристики случайного процесса. Поэтому для случайного процесса x(t) вводится понятие спектральной плотности мощности, связанной с автокорреляционной функцией преобразованием Фурье (соотношение Винера - Хинчина).
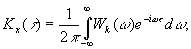
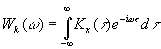 .
.
Спектральная плотность мощности определяется из последнего соотношения по функции корреляции определяемой для эргодического процесса в пределах одной реализации:
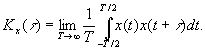
При нулевом среднем значении 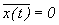 имеем:
имеем:

Чем шире энергетический спектр случайного процесса, тем быстрее меняется x(t) и меньше время корреляции, и наоборот.

 Коэффициенты такого разложения сn будут случайными величинами. Для гармонического разложения
Коэффициенты такого разложения сn будут случайными величинами. Для гармонического разложения 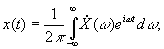
 Ввиду случайности спектральной плотности
Ввиду случайности спектральной плотности 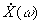 и равенства нулю ее среднего значения при усреднении по всем реализациям при
и равенства нулю ее среднего значения при усреднении по всем реализациям при  (ввиду случайности и независимости фаз спектральных составляющих в различных реализациях) она не используется для характеристики случайного процесса. Поэтому для случайного процесса x(t) вводится понятие спектральной плотности мощности, связанной с автокорреляционной функцией преобразованием Фурье (соотношение Винера - Хинчина).
(ввиду случайности и независимости фаз спектральных составляющих в различных реализациях) она не используется для характеристики случайного процесса. Поэтому для случайного процесса x(t) вводится понятие спектральной плотности мощности, связанной с автокорреляционной функцией преобразованием Фурье (соотношение Винера - Хинчина).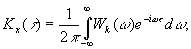
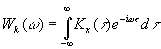 .
.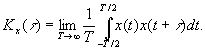
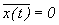 имеем:
имеем:



