Задача обеспечения минимальной погрешности при восстановлении сигнала на практике часто не ставится. Обычно указывается допустимое значение погрешности  В качестве базисных функций выбирают полиномы (степенные функции нулевого (ступенчатая), первого (линейная) и, реже, второго (параболическая) порядка). Аппроксимацию проводят на каждом шаге дискретизации, которые выбирают из условия допустимой погрешности. Вследствие того, что изменение функции
В качестве базисных функций выбирают полиномы (степенные функции нулевого (ступенчатая), первого (линейная) и, реже, второго (параболическая) порядка). Аппроксимацию проводят на каждом шаге дискретизации, которые выбирают из условия допустимой погрешности. Вследствие того, что изменение функции 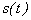 различно в различные моменты времени, шаг дискретизации может быть различным, обеспечивая равномерную погрешность на каждом шаге. Такой тип дискретизации называется адаптивный. Рассмотрим адаптивную дискретизацию при степенной аппроксимации Тейлора:
различно в различные моменты времени, шаг дискретизации может быть различным, обеспечивая равномерную погрешность на каждом шаге. Такой тип дискретизации называется адаптивный. Рассмотрим адаптивную дискретизацию при степенной аппроксимации Тейлора:

Пример 1. Аппроксимация полиномом нулевой степени (ступенчатая)
при  ,
, 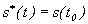 ,
, 
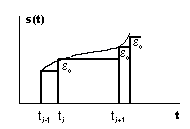
| На практике производную не определяют, а интервал дискретизации заканчивают при достижении максимального отклонения  затем сигнал скачком увеличивают до значения функции затем сигнал скачком увеличивают до значения функции 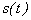 в момент окончания шага дискретизации. При восстановлении между отсчетами сигнал равен предыдущему отсчету. в момент окончания шага дискретизации. При восстановлении между отсчетами сигнал равен предыдущему отсчету.
|
Пример 2. Адаптивная аппроксимация степенным полиномом первой степени (линейная).

| На момент  каждого интервала аппроксимации принимают каждого интервала аппроксимации принимают  . Момент очередного отсчета определяется равенством . Момент очередного отсчета определяется равенством
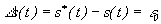 . .
|
Восстанавливают сигнал прямолинейным соединением отсчета.

 В качестве базисных функций выбирают полиномы (степенные функции нулевого (ступенчатая), первого (линейная) и, реже, второго (параболическая) порядка). Аппроксимацию проводят на каждом шаге дискретизации, которые выбирают из условия допустимой погрешности. Вследствие того, что изменение функции
В качестве базисных функций выбирают полиномы (степенные функции нулевого (ступенчатая), первого (линейная) и, реже, второго (параболическая) порядка). Аппроксимацию проводят на каждом шаге дискретизации, которые выбирают из условия допустимой погрешности. Вследствие того, что изменение функции 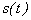 различно в различные моменты времени, шаг дискретизации может быть различным, обеспечивая равномерную погрешность на каждом шаге. Такой тип дискретизации называется адаптивный. Рассмотрим адаптивную дискретизацию при степенной аппроксимации Тейлора:
различно в различные моменты времени, шаг дискретизации может быть различным, обеспечивая равномерную погрешность на каждом шаге. Такой тип дискретизации называется адаптивный. Рассмотрим адаптивную дискретизацию при степенной аппроксимации Тейлора:
 ,
, 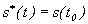 ,
, 

 затем сигнал скачком увеличивают до значения функции
затем сигнал скачком увеличивают до значения функции 
 каждого интервала аппроксимации принимают
каждого интервала аппроксимации принимают  . Момент очередного отсчета определяется равенством
. Момент очередного отсчета определяется равенством
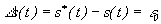 .
.



