Быстрое преобразование Фурье
Рассмотрим дискретное прямое преобразование Фурье. = 0, 1,..., -1; k = 0, 1,..., -1; j -мнимая единица. - число отсчетов. Из (1) следует, что для определения одного спектрального коэффициента При = 210 = 1024 машинное время уменьшается в 100 раз. Пусть = 2p (p - целое число). Разобьем последовательность (1) на сумму двух последовательностей, составленных из четных и нечетных номеров. Однако вычисления по (2) можно ограничить номером Аналогично Теперь снова разобьем суммы Далее суммы = 0, 1,..., 2P-3-1; для номеров +2P-3 знаки перед экспонентами заменяют на минус. Таким образом, мы имеем все время удваивающееся число сумм X,Y для одного, однако число членов в этих суммах все время в два раза уменьшается и, кроме того, в два раза уменьшается число номеров, так что общее число сумм Продолжая такое разбиение l раз, будем иметь: где l = 1, 2,..., p; i = 1, 2,..., 2l-2 в (4) и i = 1, 2,..., 2l-1 в (5). n = 0, 1,..., 2P-l-1. При l = p получим = 0, k = 0. Итак, можно предложить следующий алгоритм быстрого преобразования Фурье. Задано = 2P отсчетов сигнала for i = 1 to N/2 * for n = 0 to n = 2P-l-1. for i = 1 to i = 2l-2. l=l-1, if l>1 go to *, else for n=0 to
|

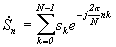 , (1)
, (1)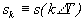 - отсчеты сигнала через интервал времени
- отсчеты сигнала через интервал времени 
 - отсчеты спектральной плотности через интервал частоты
- отсчеты спектральной плотности через интервал частоты 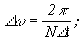
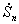 требуется умножений, вычислений экспонент и сложений, а на все коэффициентов требуется 2 умножений, сложений и вычислений экспонент. Алгоритм быстрого преобразования Фурье позволяет уменьшить число таких операций до
требуется умножений, вычислений экспонент и сложений, а на все коэффициентов требуется 2 умножений, сложений и вычислений экспонент. Алгоритм быстрого преобразования Фурье позволяет уменьшить число таких операций до 

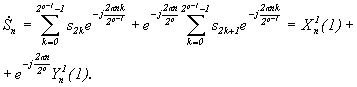 (2)
(2)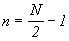 , т. к. функции
, т. к. функции  и
и 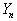 являются периодическими с периодом
являются периодическими с периодом 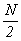 из-за большего (в два раза) интервала отсчетов между ними. Итак, при
из-за большего (в два раза) интервала отсчетов между ними. Итак, при 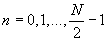 будем иметь:
будем иметь: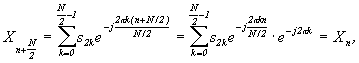 т.к.
т.к.

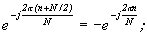
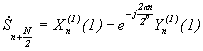 . (3)
. (3)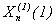 и
и 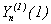 с четными и нечетными новыми номерами слагаемых:
с четными и нечетными новыми номерами слагаемых:

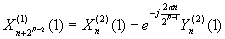 ;
;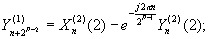 = 0, 1,..., 2P-2-1.
= 0, 1,..., 2P-2-1.
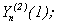
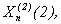
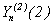 снова можно разбить. Получим:
снова можно разбить. Получим:
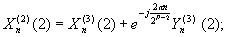


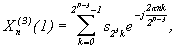 остальным членам соответствуют следующие отсчеты sk:
остальным членам соответствуют следующие отсчеты sk: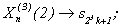




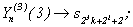
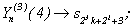 k=0,1,...2P-3-1.
k=0,1,...2P-3-1.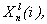
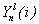 остается тем же, но уменьшается число членов в каждой сумме.
остается тем же, но уменьшается число членов в каждой сумме.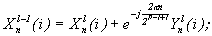
 ;
; (4)
(4) .
.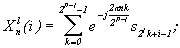
 (5)
(5)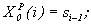
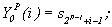 i = 1, 2,..., 2P-1.
i = 1, 2,..., 2P-1.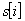 , i = 0, 1, 2,..., -1, l = p, = 0
, i = 0, 1, 2,..., -1, l = p, = 0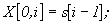
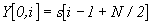 , end.
, end.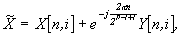

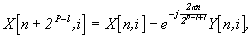

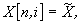
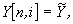 end, end.
end, end.
 , end.
, end.


