Многомерная плотность вероятности
Пусть имеем n случайных величин х1,х2, …, хn. Можно ввести n -мерную плотность вероятности p(х1,х2, …, хn), определяющую вероятность одновременного осуществления событий причем Располагая многомерной плотностью вероятности, можно находить среднее значение любых комбинаций этих случайных величин и определять их моменты. В частности, для двумерной случайной величины будем иметь: Новым по сравнению с одномерным случаем является смешанный момент второго порядка - ковариационный момент или центрированный корреляционный момент Вводят также безразмерный коэффициент корреляции Для статистически независимых случайных величин Статистически независимые случайные величины некоррелированы между собой:
|
, 
,..., 
,
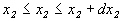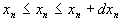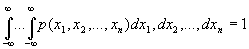. Зная n -мерную плотность вероятности, всегда можно найти m -мерную (m < n) плотность вероятности меньшего порядка, интегрируя по лишним координатам:
.
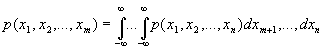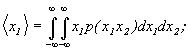
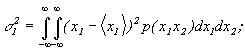
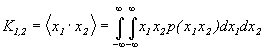
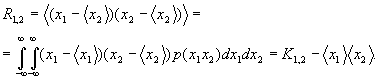
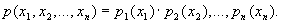
при 
. Обратное утверждение в общем случае неверно: из некоррелированности не вытекает автоматически статистическая независимость случайных величин.
