Случайный процессПод случайным процессом понимают множество (ансамбль) случайных функций хк(t), называемых возможными реализациями этого случайного процесса. В каждый выбранный момент времени t1 конкретная реализация есть случайная величина с плотностью вероятности Различают стационарные и нестационарные случайные процессы. Для стационарных процессов плотность вероятности от времени не зависит: Кроме одномерной плотности вероятности Для стационарных процессов двумерная плотность вероятности зависит только от разности моментов времени Двумерная плотность вероятности определяет дополнительный момент - автокорреляционную функцию случайного процесса. Иногда используют нормированные автокорреляционные функции: Для стационарного процесса: Если процесс не только стационарный, но и эргодический, усреднение по множеству может быть заменено усреднением по времени в пределах одной реализации: Условие эргодичности для стационарного процесса с нулевым средним значением: Это определяет стремление функции корреляции к нулю с увеличением временного сдвига t. Можно ввести интервал корреляции
|
и ее среднее значение определяется усреднением по всем возможным реализациям: 
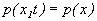. Стационарный процесс называется эргодическим, если усреднение по множеству реализаций эквивалентно усреднению по времени в пределах одной реализации.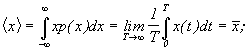
вводят двумерную плотность вероятности совместной реализации двух значений: х1 в момент времени t1 и х2 в момент времени t2.
.
.
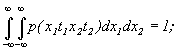
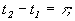
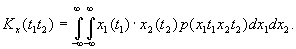
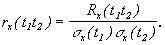
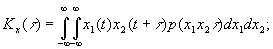
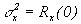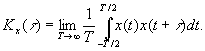
, который определяет время статистической зависимости между мгновенными значениями случайного сигнала.
