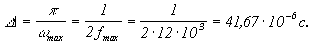Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В. А. Котельниковым: «Любая непрерывная функция s(t), спектр которой ограничен частотой Fmax полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 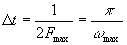 » Кроме того, теорема Котельникова дает и способ точного восстановления сигнала
» Кроме того, теорема Котельникова дает и способ точного восстановления сигнала 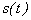 по его отсчетам.
по его отсчетам.
Доказательство
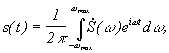 причем
причем  при
при  (1)
(1)
Разложим функцию  в частотной области на конечном интервале
в частотной области на конечном интервале  (с периодом
(с периодом 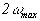 ) в комплексный ряд Фурье:
) в комплексный ряд Фурье:
 где (2)
где (2)
 (3)
(3)
Сравнивая интегралы в (3) и (1), видно, что они равны при 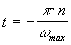 , т. е.
, т. е. 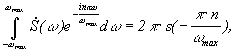 тогда
тогда
 (4)
(4)
Подставляем (4) в (2), а затем в (1)


т. к. суммирование по от -¥ до +¥, то можно заменить знак у.

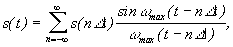
 (5)
(5)
Максимальные значения членов ряда будут при  и равны
и равны 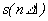 , при этом все остальные члены ряда равны нулю, т. е. при
, при этом все остальные члены ряда равны нулю, т. е. при  функция s(t) точно передается рядом. Во все другие моменты времени необходимо суммировать бесконечное число отсчетов, чтобы передать s(t) точно.
функция s(t) точно передается рядом. Во все другие моменты времени необходимо суммировать бесконечное число отсчетов, чтобы передать s(t) точно.
Представление сигнала в виде ряда Котельникова (5) является частным случаем разложения  . Роль коэффициента
. Роль коэффициента  выполняют отсчеты
выполняют отсчеты 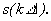 Базисными являются функции вида
Базисными являются функции вида  Они называются функциями отсчетов. Функции отсчетов ортогональны, т. к.
Они называются функциями отсчетов. Функции отсчетов ортогональны, т. к.
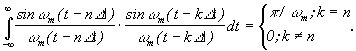
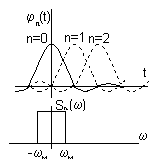
| Спектральная плотность функции отсчета на частотной шкале есть прямоугольник шириной  (идеальный фильтр н.ч.).
Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром (идеальный фильтр н.ч.).
Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром
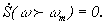
|
Такой процесс представляется (заменяется) суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов - величины выборок:
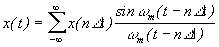 , где
, где 
Т. о., при указанных ограничениях случайный процесс полностью определяется счетным множеством случайных величин - координат процесса.
Практическое осуществление дискретизации сигнала 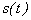 рядом Котельникова и дальнейшее его восстановление сводится к следующему. На передающей стороне через интервалы
рядом Котельникова и дальнейшее его восстановление сводится к следующему. На передающей стороне через интервалы  определяются мгновенные значения
определяются мгновенные значения 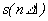 сигнала и передаются в канал связи в виде d -импульсов с площадью, равной отсчету
сигнала и передаются в канал связи в виде d -импульсов с площадью, равной отсчету  На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот
На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот 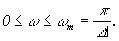 При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал
При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал 
Искажения восстановленного (по Котельникову) сигнала могут происходить по следующим причинам. Реальный сигнал имеет конечную длительность и, следовательно, обладает неограниченным спектром. Дискретизация его с интервалом 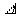 ограничивает спектр
ограничивает спектр  и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.
и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.
Несмотря на невозможность точного воспроизведения сигнала ограниченной длительности (чем более короткий сигнал, тем больше ошибка воспроизведения), дискретизация и восстановление по Котельникову используется весьма широко при преобразовании сигнала в цифровую форму.
Пример 1. Аппроксимировать прямоугольный импульс длительностью 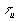 , амплитудой U рядом Котельникова, ограничивая его спектр частотой
, амплитудой U рядом Котельникова, ограничивая его спектр частотой 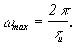 Затем восстановить сигнал по отсчетам Котельникова.
Затем восстановить сигнал по отсчетам Котельникова.

|   В нашем случае В нашем случае  и импульс аппроксимируется тремя отсчетами в моменты и импульс аппроксимируется тремя отсчетами в моменты 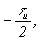 0, 0, 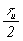 . .
|
В моменты отсчетов значения аппроксимаций совпадают с отсчетами.
Найдем значения сигналов в промежутках.
а)  ;
;
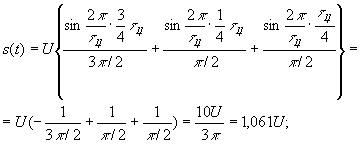
б) 
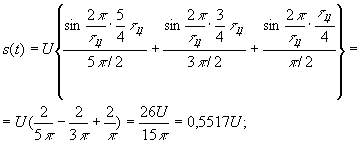
в)  ;
;
 ;
;
г)  ;
; 
д) 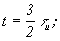

Пример 2. Сигнал звукового сопровождения в телевизионном канале ограничен верхней частотой 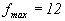 кГц. Определить интервал Dt между отсчетами этого сигнала, необходимый для неискаженного воспроизведения сигнала при передаче его дискретным способом.
кГц. Определить интервал Dt между отсчетами этого сигнала, необходимый для неискаженного воспроизведения сигнала при передаче его дискретным способом.
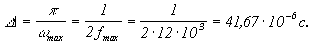

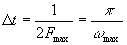 » Кроме того, теорема Котельникова дает и способ точного восстановления сигнала
» Кроме того, теорема Котельникова дает и способ точного восстановления сигнала 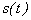 по его отсчетам.
по его отсчетам.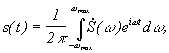 причем
причем  при
при  (1)
(1) в частотной области на конечном интервале
в частотной области на конечном интервале  (с периодом
(с периодом 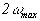 ) в комплексный ряд Фурье:
) в комплексный ряд Фурье: где (2)
где (2) (3)
(3)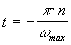 , т. е.
, т. е. 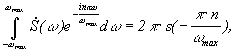 тогда
тогда (4)
(4)


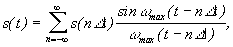
 (5)
(5) и равны
и равны 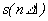 , при этом все остальные члены ряда равны нулю, т. е. при
, при этом все остальные члены ряда равны нулю, т. е. при  . Роль коэффициента
. Роль коэффициента  выполняют отсчеты
выполняют отсчеты 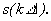 Базисными являются функции вида
Базисными являются функции вида  Они называются функциями отсчетов. Функции отсчетов ортогональны, т. к.
Они называются функциями отсчетов. Функции отсчетов ортогональны, т. к.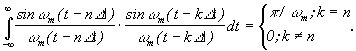

 (идеальный фильтр н.ч.).
Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром
(идеальный фильтр н.ч.).
Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром
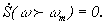
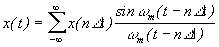 , где
, где 
 определяются мгновенные значения
определяются мгновенные значения  На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот
На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот 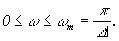 При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал
При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал 
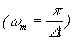 и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.
и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.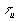 , амплитудой U рядом Котельникова, ограничивая его спектр частотой
, амплитудой U рядом Котельникова, ограничивая его спектр частотой 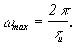 Затем восстановить сигнал по отсчетам Котельникова.
Затем восстановить сигнал по отсчетам Котельникова.

 и импульс аппроксимируется тремя отсчетами в моменты
и импульс аппроксимируется тремя отсчетами в моменты 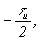 0,
0, 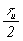 .
.
 ;
;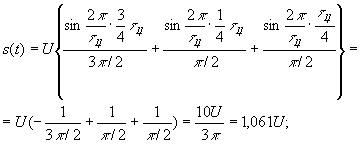

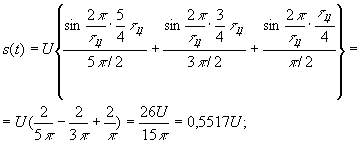
 ;
; ;
; ;
; 
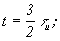

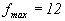 кГц. Определить интервал Dt между отсчетами этого сигнала, необходимый для неискаженного воспроизведения сигнала при передаче его дискретным способом.
кГц. Определить интервал Dt между отсчетами этого сигнала, необходимый для неискаженного воспроизведения сигнала при передаче его дискретным способом.