Дискретизированный сигнал можно рассматривать как результат умножения первоначального непрерывного сигнала на ряд единичных импульсов (d -функций).
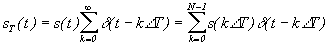 , (1)
, (1)
- общее число отсчетов;
 - отсчет, т. е. значение
- отсчет, т. е. значение 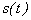 при
при 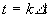 .
.
При таком рассмотрении площадь отсчета равна значению 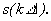 При этом существенно упрощается нахождение спектральной плотности дискретного сигнала
При этом существенно упрощается нахождение спектральной плотности дискретного сигнала  непосредственно по совокупности отсчетов
непосредственно по совокупности отсчетов  . Действительно, применив преобразование Фурье к (1), получим:
. Действительно, применив преобразование Фурье к (1), получим:
 или
или
 (2)
(2)
Спектр 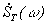 дискретизированного сигнала есть периодическая последовательность спектров
дискретизированного сигнала есть периодическая последовательность спектров  исходного непрерывного сигнала
исходного непрерывного сигнала 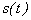 , сдвинутых относительно друг друга на
, сдвинутых относительно друг друга на  При выборе интервала дискретизации, согласно теореме Котельникова
При выборе интервала дискретизации, согласно теореме Котельникова 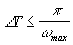 , наложения спектров этой периодической последовательности не происходит.
, наложения спектров этой периодической последовательности не происходит.
Для цифровой обработки сигналов требуется дискретизация не только во временной, но и в частотной области в основном интервале
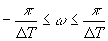 (либо
(либо 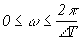 ).
).
Полагая в (2)  , где
, где  , получим:
, получим:
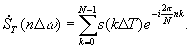 (3)
(3)
Здесь 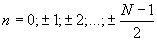 (либо
(либо  ) (=0 может не быть, если -четное). Выражение (3) называется дискретным преобразованием Фурье (ДПФ). Дискретизация спектра с интервалом
) (=0 может не быть, если -четное). Выражение (3) называется дискретным преобразованием Фурье (ДПФ). Дискретизация спектра с интервалом 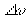 приводит к периодическому повторению сигнала с периодом
приводит к периодическому повторению сигнала с периодом 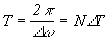 . Для обратного дискретного преобразования Фурье (ОДПФ) можно записать:
. Для обратного дискретного преобразования Фурье (ОДПФ) можно записать:
 (4) либо
(4) либо  .
.
Верность выражения (4) доказывается непосредственной подстановкой в него 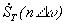 из (3) с заменой индекса суммирования k на m, сменой порядка суммирования и учетом того, что сумма
из (3) с заменой индекса суммирования k на m, сменой порядка суммирования и учетом того, что сумма 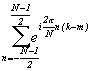 равна при k = m и равна нулю при k ¹ m как сумма векторов, которые делят окружность единичного вектора на равные дуги
равна при k = m и равна нулю при k ¹ m как сумма векторов, которые делят окружность единичного вектора на равные дуги
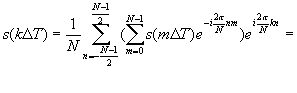

Обычно DT выбирают меньше, чем 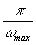 , увеличивая число отсчетов. При этом крайние значения
, увеличивая число отсчетов. При этом крайние значения  вблизи
вблизи  близки к нулю, что облегчает выделение фильтрами основного интервала
близки к нулю, что облегчает выделение фильтрами основного интервала 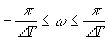 . Длительность импульсов
. Длительность импульсов 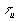 должна быть много меньше, чем
должна быть много меньше, чем  , чтобы получилась полная периодичность спектра
, чтобы получилась полная периодичность спектра 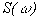 с периодом
с периодом 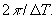 Площадь импульса должна быть пропорциональна отсчету.
Площадь импульса должна быть пропорциональна отсчету.
Отметим, что выражение (3) ДПФ при значениях вне основного интервала дает периодическое повторение дискретного спектра, а выражение (4) ОДПФ за пределами временного интервала исходного импульса дает его периодическое продолжение. Аппарат дискретного преобразования Фурье широко используется в математическом моделировании и численном математическом преобразовании.
Отметим, что смена знака w в (2) или номера в (3) не изменяет модуль 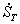 , а изменяет только знак фазы, поэтому в (3) достаточно ограничиться номерами
, а изменяет только знак фазы, поэтому в (3) достаточно ограничиться номерами  . Равенство (4) тоже можно упростить:
. Равенство (4) тоже можно упростить:  , т. к. действительные части у членов с положительным и отрицательным n совпадают, а мнимые имеют противоположный знак.
, т. к. действительные части у членов с положительным и отрицательным n совпадают, а мнимые имеют противоположный знак.

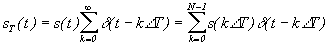 , (1)
, (1) - отсчет, т. е. значение
- отсчет, т. е. значение 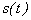 при
при 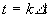 .
.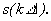 При этом существенно упрощается нахождение спектральной плотности дискретного сигнала
При этом существенно упрощается нахождение спектральной плотности дискретного сигнала  непосредственно по совокупности отсчетов
непосредственно по совокупности отсчетов  или
или (2)
(2)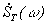 дискретизированного сигнала есть периодическая последовательность спектров
дискретизированного сигнала есть периодическая последовательность спектров  исходного непрерывного сигнала
исходного непрерывного сигнала  При выборе интервала дискретизации, согласно теореме Котельникова
При выборе интервала дискретизации, согласно теореме Котельникова 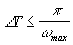 , наложения спектров этой периодической последовательности не происходит.
, наложения спектров этой периодической последовательности не происходит.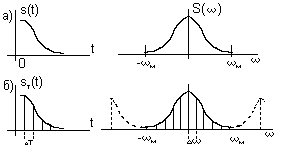
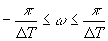 (либо
(либо 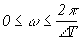 ).
). , где
, где  , получим:
, получим: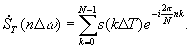 (3)
(3)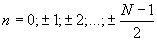 (либо
(либо  ) (=0 может не быть, если -четное). Выражение (3) называется дискретным преобразованием Фурье (ДПФ). Дискретизация спектра с интервалом
) (=0 может не быть, если -четное). Выражение (3) называется дискретным преобразованием Фурье (ДПФ). Дискретизация спектра с интервалом 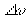 приводит к периодическому повторению сигнала с периодом
приводит к периодическому повторению сигнала с периодом 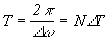 . Для обратного дискретного преобразования Фурье (ОДПФ) можно записать:
. Для обратного дискретного преобразования Фурье (ОДПФ) можно записать: (4) либо
(4) либо  .
.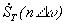 из (3) с заменой индекса суммирования k на m, сменой порядка суммирования и учетом того, что сумма
из (3) с заменой индекса суммирования k на m, сменой порядка суммирования и учетом того, что сумма 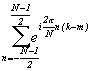 равна при k = m и равна нулю при k ¹ m как сумма векторов, которые делят окружность единичного вектора на равные дуги
равна при k = m и равна нулю при k ¹ m как сумма векторов, которые делят окружность единичного вектора на равные дуги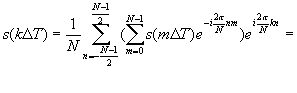

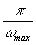 , увеличивая число отсчетов. При этом крайние значения
, увеличивая число отсчетов. При этом крайние значения  вблизи
вблизи  близки к нулю, что облегчает выделение фильтрами основного интервала
близки к нулю, что облегчает выделение фильтрами основного интервала 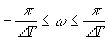 . Длительность импульсов
. Длительность импульсов 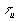 должна быть много меньше, чем
должна быть много меньше, чем  , чтобы получилась полная периодичность спектра
, чтобы получилась полная периодичность спектра 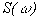 с периодом
с периодом 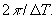 Площадь импульса должна быть пропорциональна отсчету.
Площадь импульса должна быть пропорциональна отсчету.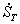 , а изменяет только знак фазы, поэтому в (3) достаточно ограничиться номерами
, а изменяет только знак фазы, поэтому в (3) достаточно ограничиться номерами  . Равенство (4) тоже можно упростить:
. Равенство (4) тоже можно упростить:  , т. к. действительные части у членов с положительным и отрицательным n совпадают, а мнимые имеют противоположный знак.
, т. к. действительные части у членов с положительным и отрицательным n совпадают, а мнимые имеют противоположный знак.


