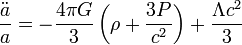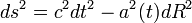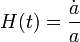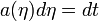Модель Фридмана
В рамках ОТО вся динамика Вселенной может быть сведена к простым дифференциальным уравнениям для масштабного фактора
Уравнению энергии
Уравнению движения
Уравнению неразрывности
k — кривизна пространства (принимает значения −1 0 1), Λ — космологическая постоянная, ρ — средняя плотность Вселенной, P — давление, с — скорость света. Для подобной модели интервал между двумя событиями записывается следующим образом:
где dR² описывает геометрические свойства пространства. В таких системах координат изменение расстояния между двумя точками (l), покоящимися в сопутствующей системе координат происходит по следующему закону:
Это не что иное, как закон Хаббла, где параметр Хаббла есть меняющаяся от времени величина:
Также в этой модели появляется различные типы расстояний: угловое и фотометрическое. Угловым расстоянием мы назовем расстояние, вычисляемое по видимому угловому расстоянию объекта (θ) и его линейному размеру объекта (D):
до какого-то момента такое расстояние увеличивается, а после начинает уменьшаться, само пространство начинает играть роль гигантской гравитационной линзы. Фотометрическое расстояние, это расстояние вычисляемое с помощью источника, известной светимости (L) и принимаемый от него поток излучения (F):
Время с начала расширения, часто называемого возрастом Вселенной:
Иногда в различного рода моделях переходят от космологического времени t к конформному η следующим образом:
|
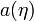
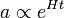
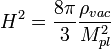
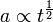
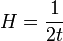
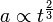
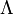-доминирование
— величины отражающая изменение расстояний в однородно сжимающихся пространствах:
