
 Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФ э электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS:
Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФ э электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS:
 . (1.3.1)
. (1.3.1)
 Знак потока dF э, очевидно, зависит от взаимной ориентации нормали и напряженности. Если эти два вектора образуют острый угол, поток положителен, если тупой – отрицателен.
Знак потока dF э, очевидно, зависит от взаимной ориентации нормали и напряженности. Если эти два вектора образуют острый угол, поток положителен, если тупой – отрицателен.
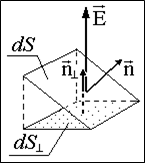
 Поток dF эчерез площадку, наклонную к силовой линии (т.е. к вектору Е),равен также потоку через проекцию этой площадки на плоскость, перпендикулярную силовой линии (см. рис. 1.3.2):
Поток dF эчерез площадку, наклонную к силовой линии (т.е. к вектору Е),равен также потоку через проекцию этой площадки на плоскость, перпендикулярную силовой линии (см. рис. 1.3.2):
 . (1.3.2)
. (1.3.2)
Это равенство (1.3.1) следует из определения (1.3.1) для dF эи теоремы об углах с взаимно перпендикулярными сторонами.

 Поток F э электрической напряженности Е через замкнутую поверхность S (рис. 1.3.3) определяется как сумма элементарных потоков через все площадки поверхности. В пределе, когда количество площадок N стремится к бесконечности, сумма потоков через площадки переходит в поверхностный интеграл от нормальной компоненты напряженности E n:
Поток F э электрической напряженности Е через замкнутую поверхность S (рис. 1.3.3) определяется как сумма элементарных потоков через все площадки поверхности. В пределе, когда количество площадок N стремится к бесконечности, сумма потоков через площадки переходит в поверхностный интеграл от нормальной компоненты напряженности E n:
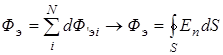 . (1.3.3.)
. (1.3.3.)
 К. Гауссом в 1844 доказана теорема (теорема Гаусса в интегральной форме), устанавливающая связь источников поля и потока напряженности через произвольную поверхность, окружающую источники.
К. Гауссом в 1844 доказана теорема (теорема Гаусса в интегральной форме), устанавливающая связь источников поля и потока напряженности через произвольную поверхность, окружающую источники.
Для доказательства выведем вспомогательную формулу. Поток от точечного заряда через произвольную окружающую его сферу.

 . (1.3.4)
. (1.3.4)
Силовые линии поля точечного заряда перпендикулярны поверхности концентрической сферы (см. рис 1.3.4). С учетом этого факта формула (1.3.4) выводится из выражения для поля точечного заряда (1.2.3). Как видно, в этом случае поток F эне зависит от радиуса сферы, а зависит только от Q.

 Из (1.3.2) и (1.3.4) следует, что поток поля точечного заряда через любую поверхность, окружающую заряд, равен потоку через сферу произвольного радиуса, концентричную заряду. Действительно, поток поля точечного заряда через любую площадку dS, вырезанную телесным углом d W из произвольной поверхности, получается таким же, как поток через площадку
Из (1.3.2) и (1.3.4) следует, что поток поля точечного заряда через любую поверхность, окружающую заряд, равен потоку через сферу произвольного радиуса, концентричную заряду. Действительно, поток поля точечного заряда через любую площадку dS, вырезанную телесным углом d W из произвольной поверхности, получается таким же, как поток через площадку  сферы, вырезанную тем же телесным углом. Поток поля F эчерез сферу, как уже отмечалось, не зависит от ее радиуса. Поэтому поток напряженности поля точечного заряда через поверхность S (см. рис. 1.3.5) задается формулой (1.3.4). Из формулы (1.3.4) и принципа суперпозиции следует теорема Гаусса в интегральной форме: полный поток F э напряженности электрического поля через произвольную замкнутую поверхность, внутри которой находится как угодно распределенный (объемный, поверхностный и т.д.) заряд Q, вычисляется по формуле
сферы, вырезанную тем же телесным углом. Поток поля F эчерез сферу, как уже отмечалось, не зависит от ее радиуса. Поэтому поток напряженности поля точечного заряда через поверхность S (см. рис. 1.3.5) задается формулой (1.3.4). Из формулы (1.3.4) и принципа суперпозиции следует теорема Гаусса в интегральной форме: полный поток F э напряженности электрического поля через произвольную замкнутую поверхность, внутри которой находится как угодно распределенный (объемный, поверхностный и т.д.) заряд Q, вычисляется по формуле
 . (1.3.5)
. (1.3.5)
При применении теоремы Гаусса для решения задач, необходимо помнить, что в уравнении (1.3.5) Q – сумма всех зарядов внутри мысленной поверхности, через которую вычисляется поток, в том числе зарядов, принадлежащим атомам и молекулам среды (так называемых связанных зарядов, см. ниже Лекция 2).
Поток напряженности поля Е через любую замкнутую поверхность,внутри которой полный заряд равен нулю, также равен нулю.


 Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФ э электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS:
Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФ э электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS: . (1.3.1)
. (1.3.1) Знак потока dF э, очевидно, зависит от взаимной ориентации нормали и напряженности. Если эти два вектора образуют острый угол, поток положителен, если тупой – отрицателен.
Знак потока dF э, очевидно, зависит от взаимной ориентации нормали и напряженности. Если эти два вектора образуют острый угол, поток положителен, если тупой – отрицателен. Поток dF эчерез площадку, наклонную к силовой линии (т.е. к вектору Е),равен также потоку через проекцию этой площадки на плоскость, перпендикулярную силовой линии (см. рис. 1.3.2):
Поток dF эчерез площадку, наклонную к силовой линии (т.е. к вектору Е),равен также потоку через проекцию этой площадки на плоскость, перпендикулярную силовой линии (см. рис. 1.3.2): . (1.3.2)
. (1.3.2)
 Поток F э электрической напряженности Е через замкнутую поверхность S (рис. 1.3.3) определяется как сумма элементарных потоков через все площадки поверхности. В пределе, когда количество площадок N стремится к бесконечности, сумма потоков через площадки переходит в поверхностный интеграл от нормальной компоненты напряженности E n:
Поток F э электрической напряженности Е через замкнутую поверхность S (рис. 1.3.3) определяется как сумма элементарных потоков через все площадки поверхности. В пределе, когда количество площадок N стремится к бесконечности, сумма потоков через площадки переходит в поверхностный интеграл от нормальной компоненты напряженности E n: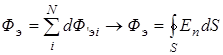 . (1.3.3.)
. (1.3.3.) К. Гауссом в 1844 доказана теорема (теорема Гаусса в интегральной форме), устанавливающая связь источников поля и потока напряженности через произвольную поверхность, окружающую источники.
К. Гауссом в 1844 доказана теорема (теорема Гаусса в интегральной форме), устанавливающая связь источников поля и потока напряженности через произвольную поверхность, окружающую источники.
 . (1.3.4)
. (1.3.4)
 Из (1.3.2) и (1.3.4) следует, что поток поля точечного заряда через любую поверхность, окружающую заряд, равен потоку через сферу произвольного радиуса, концентричную заряду. Действительно, поток поля точечного заряда через любую площадку dS, вырезанную телесным углом d W из произвольной поверхности, получается таким же, как поток через площадку
Из (1.3.2) и (1.3.4) следует, что поток поля точечного заряда через любую поверхность, окружающую заряд, равен потоку через сферу произвольного радиуса, концентричную заряду. Действительно, поток поля точечного заряда через любую площадку dS, вырезанную телесным углом d W из произвольной поверхности, получается таким же, как поток через площадку  сферы, вырезанную тем же телесным углом. Поток поля F эчерез сферу, как уже отмечалось, не зависит от ее радиуса. Поэтому поток напряженности поля точечного заряда через поверхность S (см. рис. 1.3.5) задается формулой (1.3.4). Из формулы (1.3.4) и принципа суперпозиции следует теорема Гаусса в интегральной форме: полный поток F э напряженности электрического поля через произвольную замкнутую поверхность, внутри которой находится как угодно распределенный (объемный, поверхностный и т.д.) заряд Q, вычисляется по формуле
сферы, вырезанную тем же телесным углом. Поток поля F эчерез сферу, как уже отмечалось, не зависит от ее радиуса. Поэтому поток напряженности поля точечного заряда через поверхность S (см. рис. 1.3.5) задается формулой (1.3.4). Из формулы (1.3.4) и принципа суперпозиции следует теорема Гаусса в интегральной форме: полный поток F э напряженности электрического поля через произвольную замкнутую поверхность, внутри которой находится как угодно распределенный (объемный, поверхностный и т.д.) заряд Q, вычисляется по формуле . (1.3.5)
. (1.3.5)


