Потенциальность электростатического поля. Электрический потенциал
Суммируя (интегрируя) все элементарные работы, находим что и требовалось доказать. Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным. Из принципа суперпозиции следует потенциальность электростатического поля, созданного любой системой зарядов. Из (1.6.2) и принципа суперпозиции следует также, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0: Таким образом, для любого контура в электростатическом поле циркуляция напряженности – тождественный нуль. В соответствии с утверждением (1.5.6) напряженность электростатического поля (с точностью до знака) может быть истолкована как градиент некоторой функции координат, называемой потенциалом электростатического поля Используя определение напряженности электростатического поля (1.2.1) и формулу связи между силой F и потенциальной энергией W, известную из курса механики из (1.6.4) получим, что потенциал поля в данной точке наблюдения численно равен потенциальной энергии пробного заряда q, помещаемого в данную точку, отнесенной к величине этого заряда: Потенциальная энергия электростатического поля, как и энергия поля сил тяготения, определяется с точностью до произвольной постоянной, которую можно зафиксировать выбором точки нулевого уровнядля W. Как правило, потенциальная энергия электростатического поля полагается равной нулю в бесконечно удаленной точке. Из формулы (1.6.4) путем интегрирования нетрудно получить формулу, связывающую потенциал с напряженностью: Интегрирование в (1.6.7) можно проводит по любой кривой соединяющей точки 1 и 2.
В заключение для потенциала поля точечного заряда Q приведем формулу, которая следует из сравнения формул (1.6.2) и (1.6.6) и известного из курса механики соотношения между работой A12 потенциальных сил на участке 1–2 траектории частицы и потенциальной энергией частицы в начале W1 и в конце W2 этого участка: В данном случае частицей является пробный заряд q. Формула для потенциала точки, отстоящей от точечного источника Q на расстояние r, имеет вид Рекомендуемая литература: Савельев И.В. Курс общей физики: Учеб. Пособие: для вузов. В 5 кн. Кн.2. Электричество и магнетизм – 4-е изд., перераб.– М.: Наука, Физматлит,, 1998, сс. 9–30, 41-71. Трофимова Т.И. Курс физики: Учеб. Пособие: для вузов.– 5-е изд., стер.– М.: Высш. шк., 1998, сс. 148–164. Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособие для вузов.– 2-е изд., испр. и доп.– М.: Высш. шк., 1999, сс. 182–190, 193–202. Иродов И. Е. Электромагнетизм. Основные законы.– 3-е изд., испр.–М.: Лаборатория базовых знаний, 2000, сс. 6–34. Вопросы для самоподготовки 1. Что такое электрический заряд, и какими свойствами он обладает? 2. Как описывается взаимодействие двух точечных электрических зарядов? 3. Какие физические величины и почему вводятся для описания электрического поля? 4. Как аналитически можно описать электрическое поле, создаваемое точечным электрическим зарядом? 5. Выведите формулу для напряженности электростатического поля двух точечных зарядов, одинаковых по величине и противоположных по знаку для точки наблюдения, находящейся а) посредине между зарядами, б) на расстоянии, весьма большом по сравнению с расстоянием между зарядами. 6. Что общего и в чем различие методов расчета характеристик электрического поля, создаваемого системой дискретных точечных зарядов и зарядом, непрерывно распределенным в некоторой области пространства? 7. Поясните сущность принципа суперпозициидля поля, созданного системой N зарядов. 8. Почему в большинстве случаев поле заряженных тел рассчитывают с помощью представления о пространственно распределенном заряде, а не применяют принцип суперпозиции непосредственно к точечным зарядам, создающим поле (электронам и протонам в заряженном теле), ведь тогда при вычислении поля вместо интегрирования можно было бы ограничиться обычным суммированием? 9. Докажите, что в любом силовом поле элементарный поток через площадку d S равен потоку через проекцию этой площадки, перпендикулярную вектору напряженности. Докажите, что поэтому поток поля точечного заряда через любую замкнутую поверхность, окружающую этот заряд равен потоку через любую концентричную ему сферу. 10. Покажите, что электростатическая теорема Гаусса есть следствие закона Кулона 11. Чем определяется знак потока вектора напряженности электрического поля через некоторую поверхность? 12. Изменится ли поток вектора напряженности электрического поля через замкнутую поверхность и сам вектор напряженности на поверхности, если изменить положение зарядов внутри ее? 13. Покажите, что электростатическое поле является потенциальным. 14. Покажите, что равенство нулю циркуляции вектора напряженности электростатического поля есть следствие его потенциальности. 15. Покажите, что электростатическое поле можно охарактеризовать скалярной функцией координат, называемой потенциалом. 16. Покажите, что силовые линии электростатического поля не могут быть замкнутыми. 17. Покажите, что силовые линии электростатического поля всегда перпендикулярны к эквипотенциальным поверхностям. 18. Как определить потенциал электростатического поля, если известна зависимость его напряженности от координат? 19. Как определить напряженность электростатического поля, если известна зависимость его потенциала от координат? Силовая линия, на которой находится пробный заряд показывает направление его ускорения. Откуда это следует? 20. Почему циркуляция электростатического поля по любому замкнутому контуру равна нулю? 21. Докажите, что ротор градиента любой функции координат тождественно равен нулю. 22. Рассмотрите некоторую (необязательно замкнутую) поверхность в пространстве, перпендикулярную силовым линиям электростатического поля. Используя тот факт, что на такой поверхности касательная к ней компонента напряженности равна нулю, докажите, что такая поверхность является поверхностью одинакового потенциала j = const. 23. Вспомните, как в курсе механики выводится формула для потенциальной энергии тела в поле сил земного тяготения. Выведите этим же способом выражение для потенциала поля, созданного точечным зарядом Q. Запишите общее выражение для потенциала поля, созданного объемным распределением заряда r,заданным в некоторой области V. 24. С какими новыми понятиями из математической теории векторных полей вы познакомились в этой лекции? 25. В двух противоположных вершинах углов квадрата расположены положительные заряды, а в третьей вершине – отрицательный заряд. Найти напряженность электрического поля в четвертой вершине угла, если величина каждого заряда равна 1 нКл, а сторона квадрата равна 10 см. 26. Металлической сфере радиусом 1 м сообщен заряд 1 мкКл. Определить напряженность поля в центре сферы, на ее поверхности и на расстоянии 0,5 м от поверхности. 27. Получите с помощью теоремы Гаусса напряженность поля, создаваемую бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s. 28. Две бесконечные параллельные плоскости заряжены равномерно одинаковыми зарядами с поверхностной плотностью 1 нКл / м 2. Определить напряженность поля вне пластин и между ними. 29. Две бесконечные плоскости заряжены равномерно с поверхностными плотностями зарядов s1=+2 10-7 Кл / м 2 и s2= -2·10-7 Кл / м 2 и ориентированы под углом a = 30º друг к другу. Определить напряженность поля в точке, находящейся на биссектрисе острого угла. 30. Две бесконечные плоскости заряжены равномерно с поверхностными плотностями зарядов s1=+3 10-7 Кл / м 2 и s2= – 5·10-7 Кл / м 2 ориентированы параллельно друг другу на расстоянии d =2 см. Определить разность потенциалов между точкой А, находящейся в середине между плоскостями и точкой В, находящейся на расстоянии 1 см от второй плоскости вне пространства между плоскостями. 31. Три параллельные бесконечные плоскости заряжены равномерно с поверхностными плотностями зарядов s1=10-7 Кл / м 2, s2=2·10-7 Кл / м 2 и s3=3·10-7 Кл / м 2. Расстояния между плоскостями равны d = 1 см. Определить разность потенциалов между первой и третьей плоскостями.
|


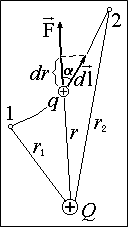 Работа поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1)это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть:
Работа поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1)это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть: 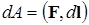 . Раскрывая скалярное произведение векторов через угол a между ними, получаем
. Раскрывая скалярное произведение векторов через угол a между ними, получаем . (1.6.1)
. (1.6.1)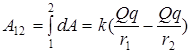 , (1.6.2)
, (1.6.2)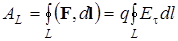 . (1.6.3)
. (1.6.3) :
: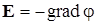 . (1.6.4)
. (1.6.4) , (1.6.5)
, (1.6.5) . (1.6.6)
. (1.6.6)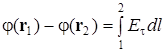 . (1.6.7)
. (1.6.7)
 Рассмотрим в пространстве, где имеется электростатическое поле, мысленную поверхность, перпендикулярную силовым линиям. При вычислении интеграла (1.6.7) по любой траектории 1–2, лежащей на этой поверхности, касательная Et компонента Е равна нулю. Следовательно, для любых двух точек 1 и 2 этой поверхности правая часть (1.6.7) равна нулю, потенциалы j(r 1) и j(r 2) одинаковы. Поверхность, во всех точках которой потенциал имеет одинаковую величину, называется эквипотенциальной. Таким образом, поверхность перпендикулярная к силовым линиям является эквипотенциальной.
Рассмотрим в пространстве, где имеется электростатическое поле, мысленную поверхность, перпендикулярную силовым линиям. При вычислении интеграла (1.6.7) по любой траектории 1–2, лежащей на этой поверхности, касательная Et компонента Е равна нулю. Следовательно, для любых двух точек 1 и 2 этой поверхности правая часть (1.6.7) равна нулю, потенциалы j(r 1) и j(r 2) одинаковы. Поверхность, во всех точках которой потенциал имеет одинаковую величину, называется эквипотенциальной. Таким образом, поверхность перпендикулярная к силовым линиям является эквипотенциальной.
 В общем случае разность потенциалов между точками 1 и 2 равна разности потенциалов эквипотенциальных поверхностей, которым принадлежат эти точки. Последнюю можно найти, проводя интегрирование в формуле (1.6.7), по силовой линии, соединяющей точки 1¢ и 2¢ этих эквипотенциальных поверхностей. При этом фактически под интегралом будет модуль Е электрической напряженности, т.к. на силовой линии
В общем случае разность потенциалов между точками 1 и 2 равна разности потенциалов эквипотенциальных поверхностей, которым принадлежат эти точки. Последнюю можно найти, проводя интегрирование в формуле (1.6.7), по силовой линии, соединяющей точки 1¢ и 2¢ этих эквипотенциальных поверхностей. При этом фактически под интегралом будет модуль Е электрической напряженности, т.к. на силовой линии  .
. . (1.6.8)
. (1.6.8)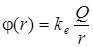 . (1.6.9)
. (1.6.9)


