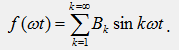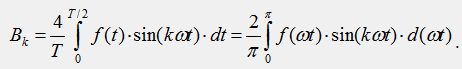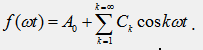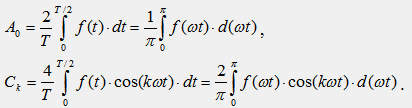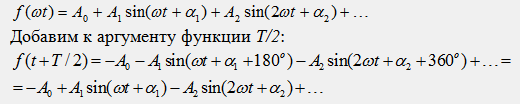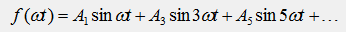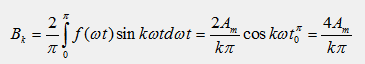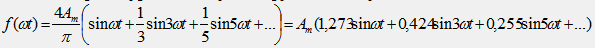Лекции по ТОЭ/ №47 Виды симметрии периодических функций.

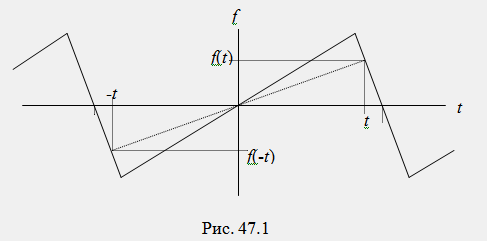
Различают следующие виды симметрии периодических несинусоидальных функций.

1) Нечетная симметрия: функция симметрична относительно начала координат и удовлетворяет условию f(t)=-f(-t) (рис. 47.1).

Функции, обладающие нечетной симметрией, получили название нечетных. В разложении таких функций содержатся только синусные составляющие отдельных гармоник Bk и отсутствуют постоянная составляющая A0 и косинусные составляющие отдельных гармоник Сk:

При определении коэффициентов ряда Фурье нечетной функции интегрирование в формуле достаточно выполнить за половину периода T/2:

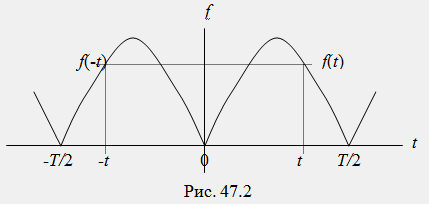
2) Четная симметрия: функция симметрична относительно оси ординат и удовлетворяет условию f(t)=f(-t) (рис. 47.2).

Функции, обладающие четной симметрией, получили название четных. В разложении таких функций содержатся только постоянная составляющая А₀ и косинусные составляющие отдельных гармоник C_k и отсутствуют синусные составляющие отдельных гармоник В_к:

При определении коэффициентов ряда Фурье четной функции интегрирование в формулах достаточно выполнить за половину периода:

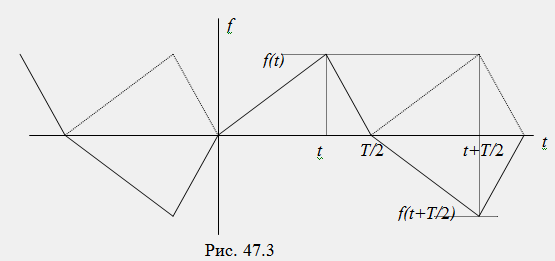
3) Косая симметрия: функция симметрична относительно оси абсцисс при смещении ее положительной части [f(t)>0] или отрицательной части [f(t)<0] на отрезок времени +-T/2 и удовлетворяет условию f(t)=-f(t+-T/2) (рис. 47.3):

Функции, обладающие косой симметрией, получили название кососим-метричных. В разложении таких функций содержатся только нечетные гармоники (синусные и косинусные составляющие):

Докажем это утверждение методом от обратного. Предположим, что кососимметричная функция содержит в разложении все члены ряда Фурье:

Равенство f(t)=-f(t+-T/2) выполняется при условии A0=0, A2=0, A4=0,…, что и требовалось доказать.

Коэффициенты ряда Фурье кососимметричной функции определяются по общим правилам.

Функция f(t) может обладать одновременно двумя видами симметрии, например, нечетной и косой или четной и косой, но не может быть одновременно нечетной и четной. При разложении конкретной функции в ряд Фурье начало отсчета следует выбрать так, чтобы получить желаемый вид симметрии функции.

 

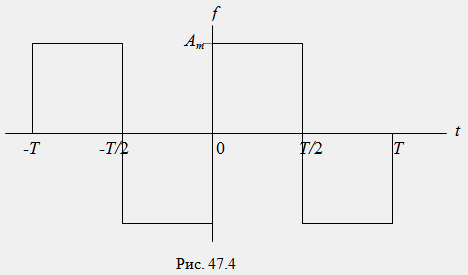
Пример. Требуется разложить в ряд Фурье периодическую прямоугольную функцию f(t)=Am(0≤t≤T/2) и f(t)=-Am(T/2≤t≤T) (рис. 47.4).

При выбранном начале отсчета (точка 0) функция будет обладать одновременно двумя видами симметрии (нечетной и косой) и ее гармонический состав будет иметь вид:

Коэффициенты ряда Фурье определяются по формуле для нечетной функции:

Тогда ряд Фурье исследуемой функции получит вид:

<div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>