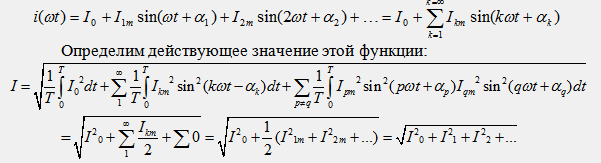Лекции по ТОЭ/ №48 Действующие значения несинусоидальных токов и напряжений.
Как известно, в электроэнергетике переменные токи и напряжения характеризуются их действующими значениями. Математически действующее значение любого периодически изменяющегося тока (напряжения) определяется как среднеквадратичное значение функции за период:
Пусть функция тока содержит в своем составе все компоненты ряда Фурье:
При интегрировании учтено, что произведение двух синусоидальных функций времени с различными частотами ω1=pω и ω2=qω дает сумму двух новых синусоидальных функций с частотами (ω1+ω2) и (ω1-ω2), определенный интеграл от которых в пределах целого числа периодов равен нулю. Итак получено, что действующее значение несинусоидального тока (напряжения) равно квадратному корню из действующих значений отдельных гармоник:
Примеры некоторых функций и их действующих значений приведены ниже:
Вывод: при коэффициенте высшей гармоники менее 0,1 (kг2=I2m/I/m ≤ 0.1) их доля в действующем значении функции составляет менее 1% (I3/I1=1.006), и, следовательно, при определении действующего значения функции с погрешностью δ<1% эти гармоники могут не учитываться. <div><img src="//mc.yandex.ru/watch/9962440" style="position:absolute; left:-9999px;" alt="" /></div>
|