Нечеткий вывод

Задача. Построить нечеткую базу знаний (использовать не менее 3 лингвистических переменных) для задачи регулирования теплоснабжения (соотношение среднесуточной температуры, ветра, размера здания и т.д.), проверить ее на полноту и произвести нечеткий вывод для конкретных значений (выбрать случайным образом).

 

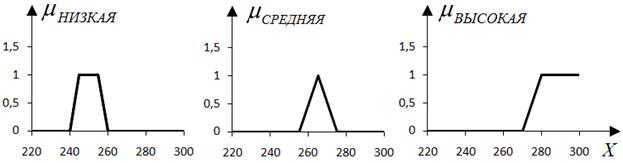
Решение

1) Предложения, описывающие задачу следующие:

· Если среднесуточная температура низкая, скорость ветра низкая или средняя, размер здания малый или средний, то потребуется слабое теплоснабжение.

· Если среднесуточная температура средняя, скорость ветра низкая, размер здания малый, то потребуется слабое теплоснабжение.

· Если среднесуточная температура средняя, скорость ветра низкая или средняя, размер здания малый или средний, то потребуется среднее теплоснабжение.

· Если среднесуточная температура высокая, скорость ветра низкая, размер здания малый, то потребуется среднее теплоснабжение.

· Если среднесуточная температура средняя, скорость ветра высокая, размер здания большой, то потребуется сильное теплоснабжение.

· Если среднесуточная температура высокая, скорость ветра средняя или высокая, размер здания большой, то потребуется сильное теплоснабжение.

Выделяем из этих предложений лингвистические переменные (определяем их через формальную запись <β,T,X,G,M>):

1. β=среднесуточная температура t=[К], T=(«высокая», «средняя», «низкая»), X=[240, 280], G=(«очень низкая», «высокая или средняя»), М – уменьшение на единицу степени принадлежность нечеткой переменной «высокая», операция объединения нечетких множеств;

2. β=скорость ветра, ϑ=[м/с], T=(«высокая», «средняя», «низкая»), X=[1, 12], G=(«очень низкая», «высокая или средняя»), М – уменьшение на единицу степени принадлежность нечеткой переменной «высокая», операция объединения нечетких множеств;

3. β=размер здания, V=[м³], T=(«малый», «средний», «большой»), X=[200, 1000], G=(«очень малый», «большой или средний»), М – уменьшение на единицу степени принадлежность нечеткой переменной «большой», операция объединения нечетких множеств.

4. β= теплоснабжение, Q=[Дж], T=(«слабое», «среднее», «сильное»), X=[20, 40], G=(«очень слабое», «сильное или среднее»), М – уменьшение на единицу степени принадлежность нечеткой переменной «сильное», операция объединения нечетких множеств.

Для полного задания лингвистической переменной определяем нечеткие переменные, входящие в Т:

Среднесуточная температура:

Скорость ветра:

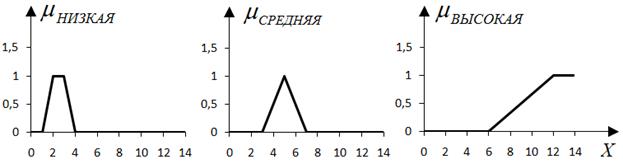
Размер здания:

Теплоснабжение:

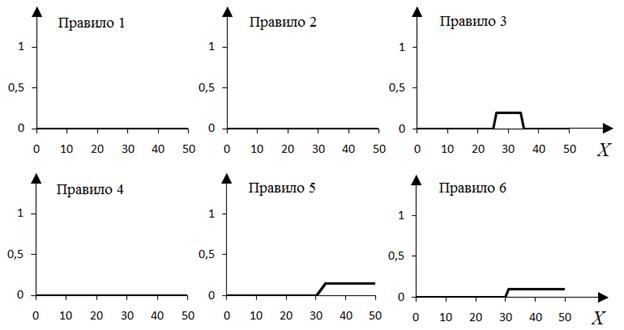
С учетом выделенных лингвистических переменных, нечеткие правила следующие:

1. Если Среднесуточная температура = «низкая», Скорость ветра = «низкая» или Скорость ветра = «средняя», Размер здания = «малый» или Размер здания = «средний», то Теплоснабжение = «слабое».

2. Если Среднесуточная температура = «средняя», Скорость ветра = «низкая», Размер здания = «малый», то Теплоснабжение = «слабое».

3. Если Среднесуточная температура = «средняя», Скорость ветра = «низкая» или Скорость ветра = «средняя», Размер здания = «малый» или Размер здания = «средний», то Теплоснабжение = «среднее».

4. Если Среднесуточная температура = «высокая», Скорость ветра = «низкая», Размер здания = «малый», то Теплоснабжение = «среднее».

5. Если Среднесуточная температура = «средняя», скорость ветра = «высокая», Размер здания = «большой», то Теплоснабжение = «Сильное».

6. Если Среднесуточная температура = «высокая», Скорость ветра = «средняя» или Скорость ветра = «высокая», Размер здания = «большой», то Теплоснабжение = «сильное».

2) Проверим полученную базу на полноту:

· существует хотя бы одно правило для каждого лингвистического терма выходной переменной – выходная переменная «Теплоснабжение» имеет 3 терма: «слабое» используется в 1 и 2 правиле, «среднее» - в 3 и 4, «сильное» - в 5 и 6;

· для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки - есть три входных переменных:

– «Среднесуточная температура», у нее три терма: «низкая» используется в 1 правиле, «средняя» - в 2, 3 и 4, «высокая» - в 5 и 6;

– «Скорость ветра», у нее три терма: «низкая» используется в 1, 2, 3 и 6 правиле, «средняя» - в 1, 3 и 5, «высокая» - в 4 и 5;

– «Размер здания», у нее три терма: «малый» используется в 1, 2, 3 и 6 правиле, «средний» - в 1 и 3, «большой» - в 4 и 5.

Значит полученная база нечетких правил полная.

3) Пусть имеется здание размером 750 м³. Определить какое количество тепла потребуется для отопления этого здания при среднесуточной температуре 271 К (-2 ᵒС) и скорости ветра 6,5 м/с.

Определим степени уверенности простейших утверждений:

Среднесуточная температура = «низкая» - 0;

Среднесуточная температура = «средняя» - 0,35;

Среднесуточная температура = «высокая» - 0,1.

Скорость ветра = «низкая» - 0;

Скорость ветра = «средняя» - 0,2;

Скорость ветра = «высокая» - 0,15;

Размер здания = «малый» - 0;

Размер здания = «средний» - 0,2;

Размер здания = «большой» - 0,35.

Определим степени уверенности посылок правил:

Правило 1: min{0, max(0, 0.2), max(0, 0.2)}=0;

Правило 2: min{0,35, 0, 0}=0;

Правило 3: min{0,35, max(0, 0.2), max(0, 0.2)}=0,2;

Правило 4: min{0.1, 0, 0}=0;

Правило 5: min{0.35, 0.15, 0.35)}=0,15;

Правило 6: min{0.1, max(0.2, 0.15), 0.35}=0,1.

Построим новую выходную нечеткую переменную, используя полученные степени уверенности:

 

4) Аккумуляция:

5) Исходя из полученного графика степени принадлежности выходного терма, можно сказать, что зданию размером 750 м³ при среднесуточной температуре 271 К (-2 ᵒС) и скорости ветра 6,5 м/с требуется для отопления не менее 26 Дж тепла (степень уверенности данного утверждения 0,2).