Тема 2 Прямоугольные проекции точек, прямой, плоской фигуры
Прочесть учебный материал, зафиксировать его в конспекте и подготовиться к закреплению материала и выполнению практического задания.
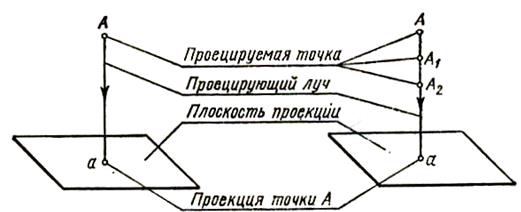
Все технические чертежи выполняются методом параллельного прямоугольного проецирования. Любой предмет можно представить как множество точек. Поэтому, чтобы выполнить прямоугольные проекции предмета, необходимо научиться находить проекции отдельных точек, принадлежащих этому предмету. На рисунке 37 дана прямоугольная проекция точки на одну плоскость, расположенную горизонтально.
Рисунок 37 – Прямоугольная проекция точки на одну плоскость
Итак, дана точка А в пространстве, из неё проведён перпендикулярно плоскости проецирующий луч до пересечения с плоскостью проекций. В результате чего получили проекцию точки а, причём точка пересечения – только одна. Но достаточно ли одной проекции, чтобы определить положение точки в пространстве? Посмотрим правую часть рисунка. На проецирующем луче Аа мы видим точки А1, А2, у которых проекция одна – это точка а. Такое изображение называется неопределённым. Значит, для определения точки в пространстве недостаточно иметь одну проекцию точки. Положение точки в пространстве будет определено, если данную точку спроецировать на две взаимно перпендикулярные плоскости проекций. Тогда определится положение точки в пространстве (рисунок 38).
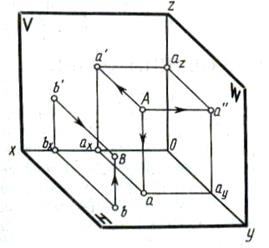
На рисунке 40а даны две взаимно перпендикулярные плоскости проекций, образующих двугранный угол. Плоскость проекций, расположенную горизонтально, принято обозначать буквой Н, а вертикальную плоскость – буквой V. Плоскости пересекаются по оси ОХ. Прямоугольную проекцию точки А на плоскость Н обозначается буквой а, на плоскости V – буквой а'. Восстановим из проекций точек а и а' перпендикуляры до взаимного пересечения и получим точку А, которая и определяет положение искомой точки в пространстве. Если повернуть плоскость Н на 90°, совместив её с плоскостью V, то вместе с плоскостью повернётся и точка а. Таким образом, фронтальная и горизонтальная проекции будут расположены на одной линии, перпендикулярной ОХ (рисунок 40б). Отрезок аха' показывает расположение точки относительно плоскости Н, а отрезок аха – относительно плоскости V. Две проекции вполне определяют положение точки относительно заданной системы плоскостей. Для изображения чертежей более сложных предметов проецирование производится на три плоскости проекций (рисунок 39).
Условимся называть (рисунок 41): - плоскость Н – горизонтальной плоскостью проекций; - плоскость V – фронтальной плоскостью проекций; - плоскость W – профильной плоскостью проекций; Плоскости Н, V, W взаимно перпендикулярны. Они образуют трёхгранный угол и составляют пространственную систему плоскостей проекций. Прямые линии х, у, z, по которым пересекаются плоскости Н, V, W,называются осями прямоугольных координат, а точка пересечения О – началом координат. На горизонтальной плоскости проекций Н получаем проекцию точки – а; На фронтальной плоскости проекций V получаем проекцию точки - а'; На профильной плоскости проекций W получаем проекцию точки - а''. Изображениями (проекциями), полученными на взаимно перпендикулярных плоскостях, пользоваться неудобно. Поэтому после получения проекций условились плоскости проекций совмещать в одну плоскость путём поворота их вокруг осей координат (рисунок 40а).
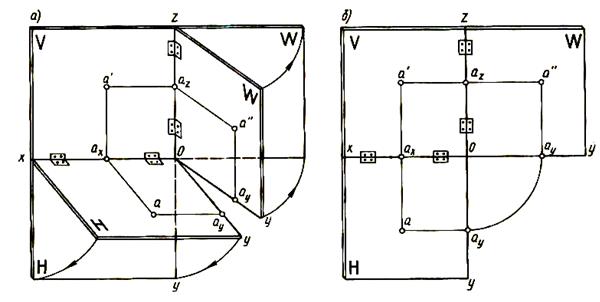
Рисунок 40 – Поворот плоскостей проекций вокруг осей координат
При этом, мысленно рассекая по оси у плоскости Н и W,вращаем плоскость Н вокруг оси х так, чтобы она, опускаясь, совместилась с плоскостью V. Плоскость W также совмещаем с плоскостью V путём поворота вправо вокруг оси z. Полученный после совмещения плоскостей проекций чертёж, состоящий из связанных между собой проекций изображаемого предмета, называется эпюром (французское название чертежа) или комплексным чертежом (рисунок 40б). Так как систему плоскостей проекций рассекли по оси у, последняя на эпюре изображается два раза: она переместится вместе с плоскостью Н вниз и будет перпендикулярна оси х, а с плоскостью W – вправо и будет перпендикулярна оси z. Дважды изображается и точка ау, которая расположена на оси у (рисунок 40б).
Для дальнейшего упрощения чертежа, показываются только оси координат х, у, z (рисунок 41).
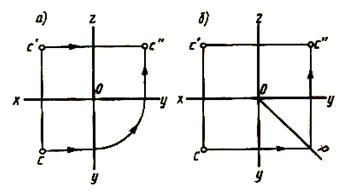
По двум заданным проекциям (горизонтальной и фронтальной) можно построить третью проекцию (профильную). Для этого из с' проводим линию связи перпендикулярно оси z,на которой будет лежать искомая профильная проекция с''. Расстояние от профильной проекции с'' до оси z равно расстоянию от горизонтальной проекции с до оси х. Это расстояние отмеряют или с помощью дуги окружности (рисунок 41а), или с помощью прямой ОР, проведённой через точку О под углом 45° к осям координат. Эта прямая носит название постоянной прямой чертежа (рисунок 41б). Расстояние от точки до плоскости W (рисунок 42) определяют координатой Х, которую называют абсциссой. Расстояние от точки до плоскости V – координату Y, называют ординатой. Расстояние до плоскости Н – координату Z, называют аппликатой.
Рисунок 42 – Координаты точки
|