Задачи и общий метод силового расчета рычажных механизмов
ВВЕДЕНИЕ
Учебным планом подготовки инженеров по специальностям 120100, 150200 в четвертом и пятом семестрах изучение дисциплины «Теория механизмов и машин», включающее выполнение курсового проекта. Цель курсового проекта состоит в изучении и практическом использовании инженерных методов анализа и синтеза механизмов различных машин и, в частности, рычажных механизмов. Проектирование таких механизмов включает в себя систему взаимосвязанных этапов, в число которых входит и силовой расчет механизмов. Методические указания содержат общую методику силового расчета плоских рычажных механизмов и алгоритм ее реализации, снабжены необходимыми теоретическими зависимостями и примерами расчетов с применением ЭВМ.
Задачи и общий метод силового расчета рычажных механизмов При работе механизма к его звеньям приложены внешние активные силы и моменты: движущие силы и моменты, совершающие положительную работу; силы и моменты сопротивления, совершающие отрицательную работу; силы тяжести подвижных звеньев и силы упругости гибких элементов (пружин и т.п.) [1,§5.1]. Под действием этих сил между элементами звеньев, образующих кинематические пары (КП), возникают внутренние силы взаимодействия (реакции связей). Вследствие движения подвижных звеньев с ускорениями на них действуют также силы инерции, которые могут быть весьма значительными в современных быстроходных машинах. Задачей силового расчета рычажного механизма является определение в его КП внутренних сил, а также оценка внешнего уравновешивающего момента, приложенного к начальному звену механизма. Для решения этой задачи применяют метод кинетостатики, основанный на принципе Даламбера [2,§5.1]: при движении механической системы приложенные к её звеньям активные силы, реакции связей и силы инерции образуют равновесную систему сил в любой момент движения. Метод кинетостатики позволяет чисто условно привести уравнения движения (динамики) механической системы к формальному совпадению с уравнениями статики (равновесия) и записать их в виде векторного уравнения сил и моментов сил относительно оси «0»:
Для учета ускореного движения подвижных звеньев в эти уравнения условно введены главные векторы
где Направление действия внутренних сил в КП, в случае силового расчета механизма без учета сил трения в этих КП, определяется по известной методике [1, c.171-178], [2, 187-190]: · в поступательной КП (1,2) сила · во вращательной КП (1,2) сила · в высшей КП (1,2) сила Уравнения (1),(2) могут использоваться для силового расчета рычажных механизмов координатным (аналитическим) или векторным (графическим) способами [2,с.198-211]. При координатном способе расчета искомые реакции связей в КП представляют в виде составляющих – проекций на оси ХОУ выбранной прямоугольной основной системы координат. При этом уравнения кинетостатики (1),(2) приводятся к виду:
При векторном способе расчета искомые реакции связей в рассматриваемой КП представляют в виде проекций на оси ХОУ прямоугольной локальной системы координат, связанной с продольной осью одного из звеньев, образующих эту КП. Реакции берутся в виде тангенциальной
Составляющая
При любом способе силового расчета механизм расчленяют и уравнения (4)-(8) составляют для статически определимых групп звеньев – структурных групп (СГ) Ассура и входящих в них звеньев. При расчленение механизма на СГ применяют принцип освобождаемости от связей – заменяют действие связей от отсоединенных звеньев в крайних КП группы реакциями, т.е. внутренними силами в этих КП.
|


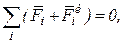 (1)
(1)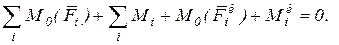 (2)
(2)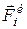 и главные моменты
и главные моменты 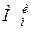 их сил инерции, выражаемые уравнениями:
их сил инерции, выражаемые уравнениями: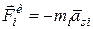 ,
, 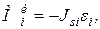 (3)
(3) масса и момент инерции i-го звена относительно оси, проходящей через его центр масс Si;
масса и момент инерции i-го звена относительно оси, проходящей через его центр масс Si;  – линейное ускорение центра масс и угловое ускорение i-го звена.
– линейное ускорение центра масс и угловое ускорение i-го звена.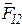 , приложенная к звену 1 от звена 2, направлена по общей нормали к соприкасающимся элементам КП на звеньях 1,2;
, приложенная к звену 1 от звена 2, направлена по общей нормали к соприкасающимся элементам КП на звеньях 1,2;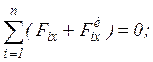 (4)
(4)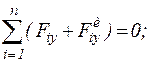 (5)
(5)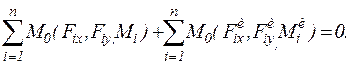 (6)
(6)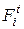 и нормальной
и нормальной 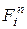 составляющих. Составляющая
составляющих. Составляющая 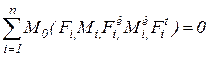 . (7)
. (7)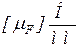 плана сил по уравнению (1) для рассматриваемой группы звеньев в виде
плана сил по уравнению (1) для рассматриваемой группы звеньев в виде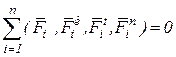 . (8)
. (8)


