Сопряжения
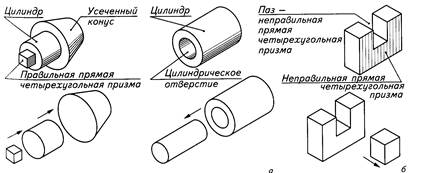
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Анализ геометрической формы объектов Анализ геометрической формы объектов – это мысленное расчленение его на отдельные части, имеющие форму геометрических тел.при анализе предмета по изображению видна только та часть предмета, которая обращена к наблюдателю (рис. 28). И важно мысленно представлять себе невидимые поверхности и элементы геометрических тел – их основания, ребра, грани и др.
Рисунок 28. Анализ геометрической формы деталей
3.2 Деление отрезков прямой, угла и окружности.
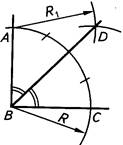
При выполнении чертежей деталей иногда приходится делить на равные части отрезки прямой линии, углы, окружности и их дуги Разделить отрезок прямой пополам можно так: из его концов проводим дуги радиусом больше половины длины этого отрезка (R>1/2 АВ). Точки пересечения дуг соединяем прямой линией, которая делит отрезок прямой на две равные части (АС = СВ) и является перпендикуляром к нему (рис. 29). На четыре равные части отрезок прямой можно разделить аналогично: вначале делим отрезок АВ пополам (АС = СВ) радиусом R>1/2 АВ, а затем каждую половину АС и СВ- еще раз пополам r>1/2 АС или r >1/2 ВС. Так можно делить отрезок на любое число равных частей, кратное четырем. При делении угла на две равные части строят биссектрису угла: - из вершины заданного угла В проводим дугу произвольного радиуса R - из точек пересечения дуги со сторонами угла (соответственно точки А и С) проводим две пересекающиеся дуги одного произвольного радиуса R R1>1/2 АС. Для построения удобнее брать радиус R1равны R, т. е. не менять радиуса на циркуле; точку их пересечения О соединяем с вершиной угла В. Угол АВС дуга АС разделились пополам (рис. 29).
Рисунок 29. Деление отрезка на равные части
Для построения чертежей некоторых деталейнеобходимо уметь делить окружность на равные части и строить правильные многоугольники. Любой диаметр делит окружность на две равные части, два взаимно перпендикулярных диаметра — на четыре
Рисунок 30. Деление угла пополам
Разделить окружности на указанное количество равных частей с помощью циркуля, построить в заданных окружностях геометрические плоские фигуры согласно образцу (рис. 31).
Рисунок 31. Деление окружности на равные части
Сопряжения Сопряжением в инженерной графике называется плавный переход от одной линии к другой непосредственно или при помощи третьей (сопрягающей) линии, а также переход от прямой линии к окружности и от окружности к окружности. Для построения сопряжений необходимы следующие элементы: радиус, центр дуги сопряжения, точки сопряжения (рис. 32, 33).
Рисунок 32. Элементы сопряжения
Рисунок 33. Алгоритм построения сопряжений
|