Fundamental Theorems on Limits
Theorem I. The limit of the algebraic sum of finitely many functions equals the sum of the limits of these functions:
Theorem II. The limit of the product of two functions equals the product of the limits of these functions:
Theorem III. The limit of the ratio of two functions equals the quotient of the limits of the numerator and the denominator:
Computations of limits. Examples. I. Limits as x ;. (1)
The limits in the numerator and the denominator equal zero. To find the limit of a linear-fractional function, we must divide the numerator and the denominator by х to the maximum power among the powers of x in the numerator and the denominator. (2) because х 4 is the maximum power of x in the numerator and the denominator. (3) A simple method for finding limits of linear-fractional functions as х is to leave the term containing the maximum power of х in the numerator and the denominator: 4)
5)
6)
Let us find limits (1), (2), (3) by the simple method:
Deleting the terms containing lower powers of x from the numerator and the denominator is only possible because, after division by х to the maximum power, the limits of all such terms vanish. II. Limits as х а. Looking for a limit, first, substitute
(1)
(2)
(3)
|

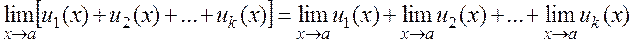 .
. .
. .
.


 (divide by х 2).
(divide by х 2). ,
,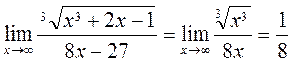 ,
, .
. ,
, ,
,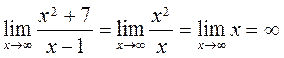 .
. in the function. If we obtain a number, then this number is the limit of the function. If we obtain one of the indeterminacies
in the function. If we obtain a number, then this number is the limit of the function. If we obtain one of the indeterminacies 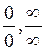 ,1, and
,1, and 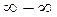 , then we must eliminate it by transforming the function and then to pass to the limit.
, then we must eliminate it by transforming the function and then to pass to the limit.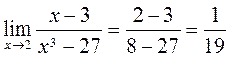 ,
,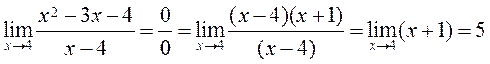 ,
, ,
,


