The infinitesimals and their properties.
Definition 1. A function (х) is called an infinitesimal as х а if
Definition 2. A function (х) is called an infinitesimal as х а if, for all х(а-; а+),
These two definitions are equivalent, i.e., we can obtain the second definition from the first and vice versa. (Prove this). Theorem I. If a function f(x) is represented as the sum of a constant number and an infinitesimal, i.e., f(x)=b+(x),(2) then it has a limit:
Conversely, if a function f(x) has limit b, then the function can be represented in the form (2). Theorem II. If (х) is an infinitesimal as х а, then Theorem III. The sum of finitely many infinitesimals is an infinitesimal: 1(х) + 2(х) + 3(х) + … + к(х)= (х). Theorem IV. The product (x).z(x) of an infinitesimal (х) by a bounded function z(x) as x a is an infinitesimal. Corollary. The product of infinitesimals is an even smaller quantity. Theorem V. An infinitesimal divided by a function having nonzero limit as х а is infinitesimal, i.e., if
|

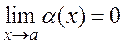 .
.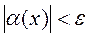 .
. .
. is an infinite quantity.
is an infinite quantity.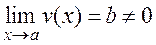 , then
, then  is an infinitesimal.
is an infinitesimal.