The limit of a sequence.
Definition. A sequence is an infinite set of terms, each of which is assigned a number. The terms of a sequence must obey a certain law. х 1, х 2, х 3, х 4, …, хn,…. Example.
Definition. A number а is called the limit of a sequence if, for any >0, there exists a number N() depending on , such
Notation:
Example.
Definition. The limit of a variable х is a number а such that for any >0, there exists an х starting with which all х satisfy the inequalities
Notation:
а– а а+ х (а–; а+) Properties: 1. The limit of a constant number equals this number. 2. A variable can not have two different limits. 3. Some variables have no limit. Example. Definition. We saythat х tends to infinity if, for any number М, there exists an х such that, starting it,
(a) M> 0, x>M, x ; (b) M< 0, x<–M, x –. Example. xn=n2+1; as n , хn tends to infinity. The limit of a function. Suppose that y=f(x) is a function defined on a domain D containing a point а: аD. Definition. A number b is called the limit of the function f(x) as х а if, for any given >0, there exists a small positive depending on (()>0) such that, for any х satisfying the inequality
Example. Find the limit of f(x)=5x–1 as x2, and determine .
i.e., To find , we must find x from the inequality for the function and substitute it in the inequality for the variable. Definition. The left limit of a function f(x) as x a is the limit of f(x) as x a, and х<а. Notation:
Definition. The right limit of a function f(x) as x a, is the limit of f(x) as x a, and х>а. Notation:
If the left limit equals the right limit and some number b, then b is the limit of the function as x a. Example.
Definition. A number b is called the limit of f(x) as х if, for any >0, there exists a (large) number N depending on such that Notation:
|
for n>N,
.
.
.
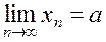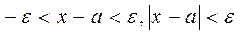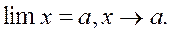
2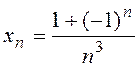
. Assigning integer values to n, we obtain: 
etc.; i.e. this variable has no limit.
.
, 
. Notation: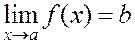
. (1)
,
,
.
.
.
; 
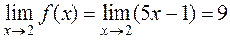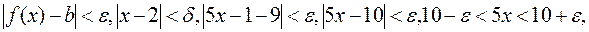
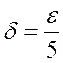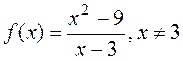an indeterminacy, although the limit exists: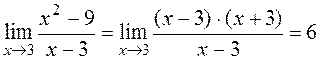
.
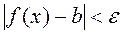for any 
.
.
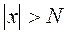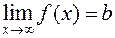