Asymptotes of a Hyperbola
Definition. The asymptote of a curve is a straight line approached by the curve line at infinity. An oblique asymptote is determined by an equation of the form an oblique y=kx+b. To find the slope, we suppose that b =0; then
We find b from the equation Passing to the limit, we obtain
Thus, the hyperbola has two asymptotes, passing through the origin:
First, we construct a rectangle with sides 2 а along the х- axis and 2 b along the у- axis. We draw the diagonals in this rectangle and extend them; they are the asymptotes of the hyperbola.
2a 2b
F1 М1(–а;0) 0 М2(а;0) F2 x
From the vertices M1 (– a;0) and M2 (a;0), we draw the branches of the hyperbola approaching the asymptotes. The directrices of a hyperbola. By definition,
|
; 
.
.
; 
.
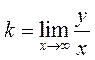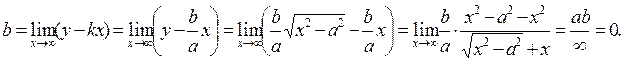
y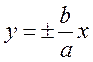 
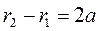. By analogy with an ellipse, we find the difference of squares
,
.
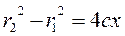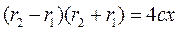