Ellipse
Definition. An ellipseis the locus of points for which the sum of distances to two fixed points is constant and equal to 2 а. Take two fixed points at a distance 2c apart, join them by a straight line, and extend this line to the x -axis. We draw the perpendicular line through the center of the segment between the focuses and take it for one coordinate axis. Let us derive the equation of the ellipse.
у M4( 0; b) r1 М(х;у) r2 M1(–a; 0 ) F1 (–c; 0 ) 0 F2 (c; 0 ) M2(a; 0 ) х M3( 0; –b)
The points F 1 and F 2 are called the foci of the ellipse, and r 1 and r 2 are its focal radii. To derive the equation of an ellipse, we take an arbitrary point М(х,у) and consider the distances to the foci:
The characteristic feature of this line is, by definition,
This is the equation of the ellipse. Let us reduce it to a convenient form:
Eliminating some terms and reducing by 4, we obtain
Let us square both sides:
We obtain
Let us divide both sides by
changing the sign, we obtain the equation of the ellipse:
Since the length 2 a of a polygonal line is larger than the length 2 c of a straight line, we can denote the difference of squares by
Thus, we obtain the classical equation of an ellipse:
|



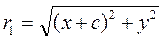 ,
, 
 .
.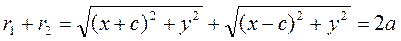 .
. ,
,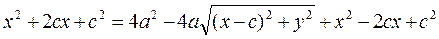 .
.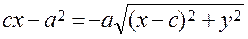 .
.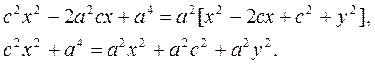
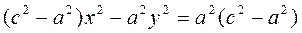 .
. :
: ;
;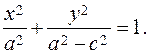
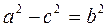 . (*)
. (*) . (17)
. (17)