Tangents to an EllipseConsider the equation of an ellipse:
М0(х0;у0)
х
As is known, the equation of a tangent to a curve is determined by the formula
Differentiating the equation of the ellipse as an implicit function, we obtain Substituting this k,we find the equation of the tangent line:
Let us transform it:
Since the point М 0 belongs to the ellipse, the coordinates of М 0 must satisfy its equation, and the right-hand side equals one. Thus, the equation of a tangent to an ellipse is
Example. Given the ellipse given Let us reduce the equation it to the classical form (17):
Let us find the eccentricity:
The equations of the directrices are
|
у 
.
.
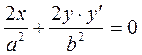, whence 
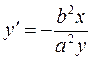, or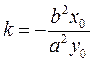 
.
.
,
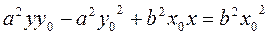. Dividing by 
, we obtain
.
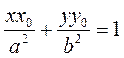. (18)
, find the distance between its foci, eccentricity, and the equations of directrices.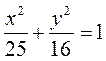
; 
;
, 
.
, 
.
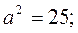
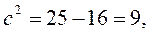
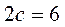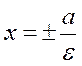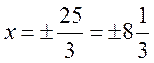