As a result, we obtain
By definition,
y
M1(–а;0) 0 M2(а;0) x
Since the eccentricity of a hyperbola is The ratios of the focal radii to the corresponding distances from an arbitrary point of the hyperbola to the directrices is constant and equals the eccentricity:
Tangent lines to a hyperbola. Suppose given, the equation of a hyperbola and a point М0(х0,у0) on it:
As is known, the equation of a tangent to a curve is
Let us differentiate the equation of a hyperbola as an implicit function:
Substituting, we obtain the equation of the tangent line:
Let us transform it:
Since the point М 0 belongs to the hyperbola, its coordinates must satisfy the equation of the hyperbola, and, the right-hand side equals (–1). Thus, the equation of a tangent to a hyperbola is
Example. Write the equation of the hyperbola with real semi axis 4 and foci at the points F 1(– 5;0) and F 2(5;0). Formula (19) gives
We have The required classical equation of the hyperbola is
|

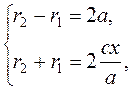
 ;
; 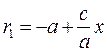 .
.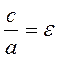 is the eccentricity of the hyperbola; we have
is the eccentricity of the hyperbola; we have 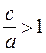 , because с> а.
, because с> а.

 and
and  .
.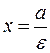


 , it follows that the directrix is
, it follows that the directrix is 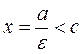 ; i.e., the directrices lie between the two vertices.
; i.e., the directrices lie between the two vertices. .
. .
.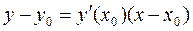 .
. ; we obtain
; we obtain  , or
, or  .
. ,
,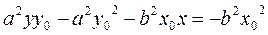 ;
; . Dividing by
. Dividing by 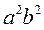 , we obtain
, we obtain .
.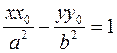 .
.
 and
and 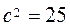 ; thus
; thus 
 –
–  =25–16=9.
=25–16=9. .
.


