Intersection points of an ellipse with the coordinates axes. To find the intersection points of an ellipse with the x-axis, we must solve the system of equations
We obtain two vertices of the ellipse: М 1(–а; 0), М 2(а; 0),
а is the major semi axis We find the intersection of the ellipse with the y -axis by solving the system
We obtain the two other vertices of the ellipse, М 3(0;– b) and М 4(0; b).
b is the minor semi axis. It is seen from equation (17) and the figure that the ellipse is symmetric with respect to the axes Ox and The eccentricity and directrix of an ellipse. Consider the focal radii of an ellipse
By definition, we have
Consider the difference of squares
or
d1 М(х;у) d2
F1(–c; 0 ) 0 F2(c; 0 ) x
x =– l x = l
to determine the focal radii, we solve the system of equations
Definition. The ratio of distances between the foci to the sum of focal radii is called eccentricity:
If the distance between the foci is less than 2 а, then the eccentricity is Thus, the focal radii of the ellipse are
Definition. The directrix of an ellipse is the straight line parallel to the y -axis such that the ratio of the focal radius to the distance from an ellipse point to it is constant and equal the eccentricity. Let us draw two straight lines x=–l and x=l parallel to the y -axis and find l such that the ratio of the focal radius to the distance from a point М to this straight line is constant and equals the eccentricity:
Substituting the distance and the focal radius, we obtain
The ratio is equal to the eccentricity when
where
|

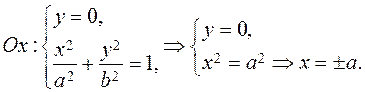
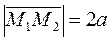 is called the major axis of the ellipse;
is called the major axis of the ellipse;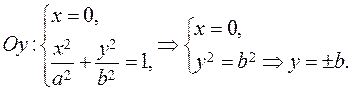
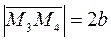 is called the minor axis of the ellipse, and
is called the minor axis of the ellipse, and .
. ;
; 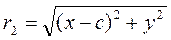 .
.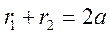 .
.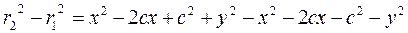 ;
;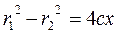 ,
,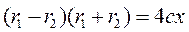 .
. y
y r1 r2
r1 r2 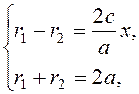
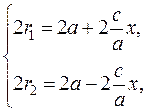 or
or 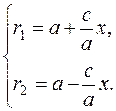
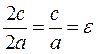 .
.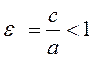 .
.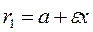 ,
,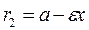 .
.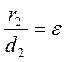 .
.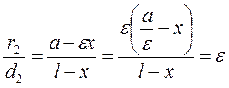 .
.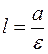 , i.e.,
, i.e., 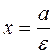 is the directrix. By analogy, we obtain equations of the directrices:
is the directrix. By analogy, we obtain equations of the directrices: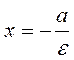 ;
; 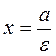 ,
,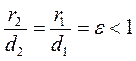 .
.


