Vector Product and Its Properties
Definition. The vector product of two vectors (1) the absolute value of
(2) the vector
(3) the three vectors
1.The absolute value of the vector product of two vectors is equal to the area of the parallelogram spanned by these vectors:
2. The vector product is anticommutative, i.e.,
3. To multiply a vector product by a number l, it is suffices to multiply one of the vectors by this number (without proof):
4. Vector product is associative:
5. The vector product of collinear vectors is equal to zero, and vice versa, if the vector product of two vectors is zero, then these vectors are collinear.
|
Consider two vectors 
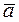and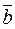 
:
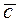, satisfying the following conditions:
equals the product of the absolute values of the two given vectors and the sine of the angle between them: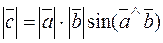
; (*)
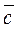is perpendicular to both vectors 
;
.
.
.
.
.
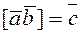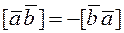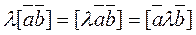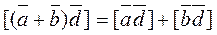