Decomposition of vectors.
Theorem 1. An arbitrary vector
Theorem 2. An arbitrary vector
Let The Cartesian system of coordinates. Consider the following coordinate system: take mutually perpendicular unit vectors
Definition. The triple of vectors From the triangle ОММ1, we obtain
Since the vector
From the triangle ОАМ1 , we obtain
because, by analogy, the vectors
Thus, the radius vector Consider the vectors
and their sum
Under addition the respective coordinates are added Let us multiply the vector
When a vector is multiplied by a number l, each coordinate of this vector is multiplied by this number. Example. Find the vector
Let us find the required vector in vector notation:
To find the same vector in vector notation, we multiply the first vector by 4 and the second by –3 and sum their coordinates:
Given two points Thus, we have found the required vector in the coordinate notation:
To find the coordinates of a vector, we must subtract the coordinates of its tail from the coordinates of the head. For example, let us find vectors with given coordinates of heads and tails: М 1(7;4;–3); М 2(1;–2;–2);
Find the length of a vector
From the right triangle ОМ 1 М 2, we find the hypotenuse
where M 1 From the other right triangle ОАМ 2, 0 z1 y we find the hypotenuse Substituting it into А x 1 the first hypotenuse, we obtain x y 1 M 2
Thus, the length of a vector is defined by the formula
|

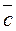 in the plane can be decomposed into two noncollinear vectors:
in the plane can be decomposed into two noncollinear vectors: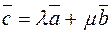 .
.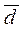 in space can be decomposed into three noncoplanar vectors
in space can be decomposed into three noncoplanar vectors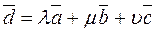 .
.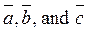 be noncoplanar vectors.
be noncoplanar vectors.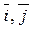 and
and 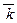 , draw coordinate axes x,y and z along them, and fix a unit on metric scale:
, draw coordinate axes x,y and z along them, and fix a unit on metric scale:
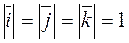 ,
,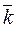
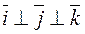 .
.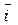

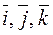 is called right if, looking from the endpoint of the last vector, we see that the shorter rotation from the first vector to the second is anticlockwise.
is called right if, looking from the endpoint of the last vector, we see that the shorter rotation from the first vector to the second is anticlockwise.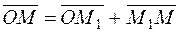 ,
,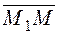 is collinear to the unit vector
is collinear to the unit vector  , it follows that
, it follows that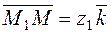 .
.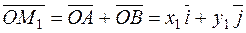 ,
,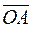 and
and 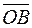 are collinear to the unit vectors
are collinear to the unit vectors 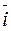 and
and 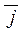 . Substituting the vector
. Substituting the vector 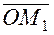 thus obtained, we see that
thus obtained, we see that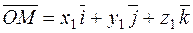 . (2)
. (2)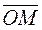 is represented as the sum of
is represented as the sum of 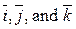 and multiplied by the corresponding coordinates of the point М.
and multiplied by the corresponding coordinates of the point М. and
and 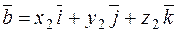
 .
. by a number l:
by a number l: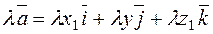 .
.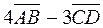 if
if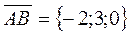 ;
; 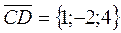 .
.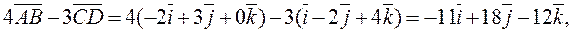
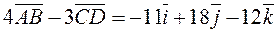 .
.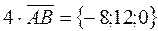

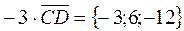
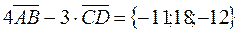 .
.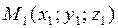 and
and 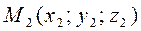 in space, find the vector
in space, find the vector  .
.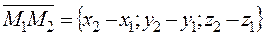 . (2¢¢)
. (2¢¢)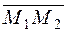 ={–6; –6; 1};
={–6; –6; 1}; 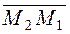 ={6; 6; –1}.
={6; 6; –1}.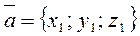 :
: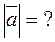
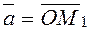 .
.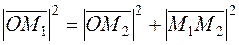 ,
, z
z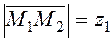 .
.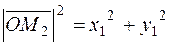 .
.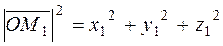 .
.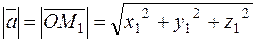 . (3)
. (3)


