Inner Product of Vectors and its Properties
Definition. The inner product of two vectors
0 φ В Property 1. Theinner product of two vectors is equal to the product of the absolute value of one vector and the projection of the second vector onto the first, i.e.,
Property 2. The inner product of two vectors is equal to zero if and only if these vectors are perpendicular.
Property 3. The inner product of vectors is commutative:
Property 4. To multiply an inner product by a number l, it is sufficient to multiply one of the factors by l:
Property 5. Inner product is associative:
|
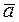and 
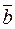is the product of the absolute values of these vectors and the cosine of the angle between them:
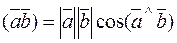. (4)
A
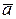
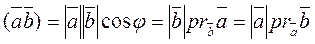. (5)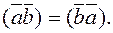
.
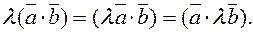
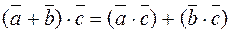