Consider two vectors
Thus, six of the nine terms are zero, and the remaining three terms are
The inner product of vectors is equal to the sum of products of their coordinates. Example 1. Example 2.
Let us derive a formula for the length of a vector by using inner product:
By (6), it equals
Thus, we obtain
The direction of a vector. Let us find the angle between two vectors Consider the inner product
We have
Writing the product and absolute values in coordinates, we obtain
Example 3. Find an angle between vectors
Let us determine a condition for vectors to be perpendicular. Suppose that vectors
z
x Consider the angles between a vector
Take the product of
By formula (*), the cosine of the angle a from it is
Similarly the cosines of the other angles are
These cosines are called the directional cosines of the vector The sum of the squared directional cosines equals one:
To prove this, it sufficies to square the cosines by formula (8) and sum them:
Example 5. For what a are the vectors
perpendicular? We use the perpendicularity condition (7) and write the inner product of the given vectors in coordinates:
|

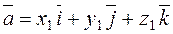 and
and 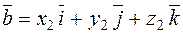 .
.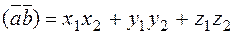 . (6)
. (6) -?
-?  and
and  , then
, then  .
. and
and  . Then
. Then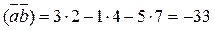 .
.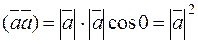 .
. .
. .
.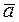 and
and 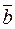 .
. .
. . (*)
. (*) . (**)
. (**) and
and 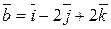 . By using formula (**), we find
. By using formula (**), we find ,
, 
 ; then
; then  , and
, and . (7)
. (7) This is the condition for vectors to be perpendicular.
This is the condition for vectors to be perpendicular.

 0
0  y
y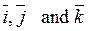 . We denote these angles by
. We denote these angles by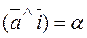 ;
; 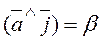 ;
; 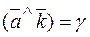 .
. and any unit vector, say,
and any unit vector, say,  =
= 
 .
. .
. ,
, 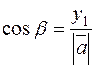 ,
,  . (8)
. (8)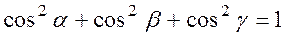 .
.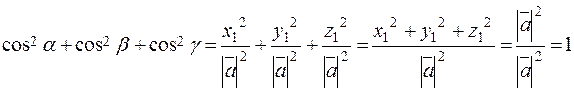 .
. and
and 
 ;
;  , a=10.
, a=10.