Linear Operations on Vectors
Definition. The product of a vector (1) (2) The vector 3. The vectors
Property 1. For any numbers α and β and any vector α (β
Definition. Suppose that
C
Property 2. Addition of vectors is commutative; this means that, for any two vectors,
Property 3. Addition of vectors is associative; this means that, for any vectors,
Property 4. Addition is distributive with respect to multiplication by a number; i.e., for any vectors
Property 5. For any numbers a and b and any vector
Definition. Free vectors are vectors which can be translated, which means that they do not depend on the head but are determined by direction and length. B
A A1 A Consider vectors
Definition. The ort-vector of a vector
Subtraction of vectors can be considered as the addition of two vectors, the second of which is taken with the sign –:
Definition. The projection of a vector onto an axis is defined as the length of the interval whose endpoints are the projections of the endpoints of the vector onto this axis which is taken with the sign + if the angle between the vector and the axis is acute and with this sign – if this angle is obtuse:
|

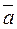 and a real number lis the vector
and a real number lis the vector 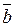 defined by the following conditions:
defined by the following conditions: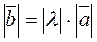 ;
;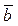 is collinear to
is collinear to 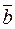 and
and 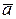

 3
3 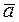 ,
,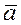 )=(αβ)
)=(αβ) 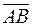 and
and 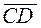 are vectors and E is a point such that
are vectors and E is a point such that 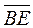 =
=  . Then the vector
. Then the vector 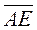 is called the sum of the vectors
is called the sum of the vectors 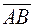 and
and 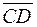 and denoted by
and denoted by  E
E 

 ε
ε
 В
В 



 =
=  .
.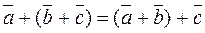 .
. and any number a,
and any number a, .
. ,
,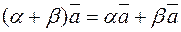 .
.

 B1 B
B1 B , their sum
, their sum 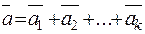 is determined by one vector, whose head coincides with that of the first vector and the tail with that of the last vector.
is determined by one vector, whose head coincides with that of the first vector and the tail with that of the last vector.



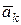
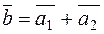 ,
,
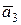
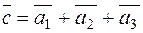 .
.

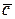

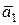

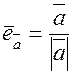 is the ort-vector of
is the ort-vector of 

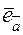
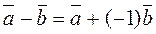 .
. .
.


