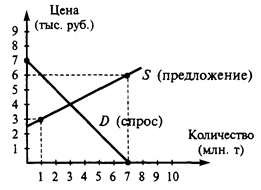
Consider vectors
Note that the right – hand side is the expansion of a third – order determinant along the row with elements Thus, the coordinates of the vector product are determined form the third – order determinant as
and its absolute value is
Example 1. Given the vectors (а) Let us use the expression (9) a vector product:
(b) Let us find the required product by using associativity:
Since the second product is expressed linearly in terms of the first, it sufficed to multiply the coordinates of the first vector by 4:
|
and 
.
and 
.
, (9)
.
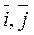and 
, find the vector products (а) 
; (b) 
.
= 
,
= 
.
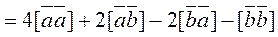
, whence 
. 
