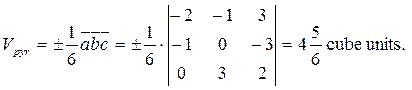Triple Product of Vectors and its Properties
Definition. Thetriple product of three vectors is the inner product of the third vector by the vector product of the first two vectors; it is denoted by
Definition. The vector product of the vector product of the first two vectors and the third vector ones is called the double vector product:
Since double vector product is used very rarely, it have been little studied. Property 1. The triple product of three vectors equals the volume of a parallelepiped spanned by these three vectors. Corollary. It is easy to derive an expression for the volume of a pyramid from the formula: S
B
А Vрyr= Vрyr= The sign Property 2. Triple product is commutative, and
Property 3. A constant multiplier of any vector can be factored out of scalar triple product:
Triple Product in Coordinates. Given three vectors
The vector product equals
Taking its inner product with
this is a third – order determinant expanded along the last line, i.e.,
Thus, the triple product of three vectors equals the third – order determinant of the composed of the coordinates of these vectors. Example 1. Determine the volume of a pyramid ABCD from the coordinates of its vertices.
Let us find the volume of a pyramid by the formulas proved above:
|
.
.
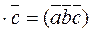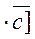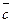
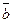
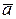С
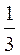Sbase Н = 
. 
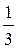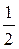Sрar Н = 
Vрar= 
,
.
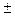is needed to obtain a positive volume.
.
.
, 
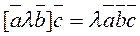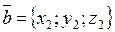, and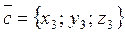 
, let us express the triple product of these vectors in terms of their coordinates. Consider the triple product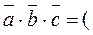
.
.
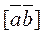
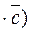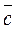, we obtain
;
.
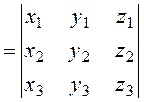D (1;5;2)
B (–1;1;3)
A (1;2;0)
C (0;2;–3)
,
,
.
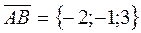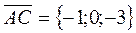