Infinitesimals and bounded functions.
Definition. A function f(x) is said to be infinitesimals as х а if, for any М, there exists a such that
Notation:
Definitions. 1. A function f(x) is said to be bounded on a domain D if, for any х from D, |f(x)|M.
For example, f(x)= cos x, | cos x| 1, M= 1,
If this condition is not satisfied, then the function is said to be unbounded, i.e., this function is an infinite quantity. 2. A function f(x) is said to be bounded as х а if, for any х from a neighborhood of а, |f(x)|M. 3. A function f(x) is said to be bounded as х if, for any х>N, |f(x)|M. Theorem I. If a function f(x) has a finite limit as xa then f(x) is bounded as x a. Theorem II. If a function has a limit as х а and this limit is not equal to zero, then
|
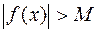whenever 
.
.
.
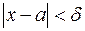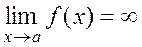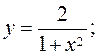
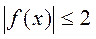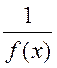is bounded as х а.
