The First Remarkable Limit and Its Generalization
The following limit exists and equals 1:
Example: (1) 2)
The first generalized remarkable limit. The first remarkable limit can be generalized, namely, written in the more general form
In this formula, (х) is an infinitesimal; it is very important that the argument of the sine and the denominator must be absolutely identical. Examples. (1)
(2)
|

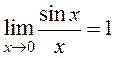 .
.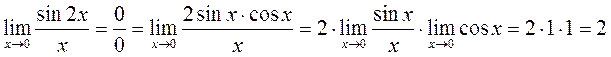 ,
, .
. (4)
(4)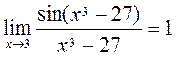 ,
,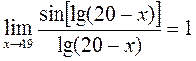 .
.


