Измерение сопротивлений при помощи мостовой схемы
Принадлежности: источник постоянного тока, три магазина сопротивлений, два резистора с неизвестным сопротивлением, нуль-гальванометр, ключ, соединительные провода. Краткая теория. Ток в металлическом проводнике согласно закону Ома пропорционален приложенному к проводнику напряжению
Коэффициент пропорциональности В металлических проводниках электропроводность обусловлена наличием свободных электронов (электронов проводимости). По современным воззрениям такого рода электронами являются валентные электроны атомов металла, наиболее слабо связанные с ядрами атомов. Вещества, которые хорошо проводят электрический ток лишь при определенных условиях, составляют группу полупроводников. Плохой проводимостью обладают диэлектрики: их проводимость в Электрическое сопротивление зависит от рода вещества проводника, от его геометрических размеров и формы, а также от состояния (например, температуры). Для проводников цилиндрической формы постоянного поперечного сечения
где Величина
Здесь
Существуют различные способы измерения сопротивлений. Простейшим из них является измерение при помощи амперметра
Более точно измерить сопротивление можно при помощи мостовой схемы. В случае, когда электрическая цепь состоит из большого числа соединенных между собой резисторов, но имеет при этом один источник тока, ее можно упростить, исходя из правил расчета сопротивлений при их последовательном и параллельном соединении. В конечном счете, получается схема, подобная рис. 1, и расчет ведется по закону Ома для замкнутой цепи. Если схема содержит не один источник тока (рис. 3) или собрана в виде моста (рис. 4), использование закона Ома невозможно, однако расчет можно выполнить, если воспользоваться правилами Кирхгофа. Этих правил два.
Первое правило Кирхгофа касается узлов цепи (узлом называется точка, в которой сходится более чем два проводника, рис. 2) и гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
Справедливость этого утверждения вытекает из следующих соображений. Если бы алгебраическая сумма токов была отлична от нуля, в узле происходило бы накапливание или уменьшение заряда, что в свою очередь приводило бы к изменению потенциала узла и изменению текущих в цепи токов. Таким образом, чтобы токи в цепи были постоянными, должно выполняться условие (4). При этом ток, текущий к узлу, считается имеющим один знак (например, плюс), ток, текущий от узла – другой знак. Уравнение (4) можно написать для каждого из
Применим правила Кирхгофа к схеме рис. 3. В различных участках цепи протекают неизвестные токи
В уравнении (5) номера токов соответствуют номерам сопротивлений, через которые эти токи текут, и входящие в узел токи считаются положительными. По второму правилу Кирхгофа алгебраическая сумма падений напряжений на участках замкнутого контура равна алгебраической сумме ЭДС, включенных в этот контур:
Чтобы записать уравнения по второму правилу, необходимо выделить независимые контуры и задать направление их обхода (на рис.3 направление обхода контуров Для контуров
Уравнения могут быть составлены для всех замкнутых контуров, которые можно выделить в конкретной разветвленной цепи. Но независимыми будут уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга. В рассмотренной на рис. 3 схеме третий контур получается наложением первых двух. Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же ЭДС войдет в разные уравнения с различными знаками. Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении на противоположные.
Составляя уравнения, следует помнить, что через любую ветвь цепи течет только один ток (под ветвью понимается участок цепи между двумя узлами). Число независимых уравнений, составляемых в соответствии с правилами Кирхгофа, оказывается равным числу токов, текущих в различных ветвях разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи. Схема на рис.3 имеет три тока, поэтому для решения достаточно системы, состоящей из уравнений (6) и (7). Мостовая схема представляет собой замкнутый четырехугольник Используя правила Кирхгофа, запишем систему уравнений для выделенных узлов и контуров неуравновешенного (
Схема (рис. 4) содержит шесть независимых токов (шесть ветвей), для нахождения которых достаточно системы уравнений (8). Сопротивления
Из (9) легко найти соотношение:
Если известны значения трех сопротивлений, например,
В качестве неизвестного сопротивления
|

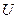 (при условии, что температура проводника остается постоянной):
(при условии, что температура проводника остается постоянной): .
.
 есть электропроводность (или проводимость) проводника,
есть электропроводность (или проводимость) проводника, 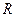 – электрическое сопротивление.
– электрическое сопротивление. раз ниже электропроводности проводников.
раз ниже электропроводности проводников. эта зависимость наиболее проста:
эта зависимость наиболее проста: ,
,
 – удельное сопротивление,
– удельное сопротивление,  – длина проводника.
– длина проводника. называется удельной электропроводностью. Значение удельного сопротивления
называется удельной электропроводностью. Значение удельного сопротивления  .
.
 – удельное сопротивление при
– удельное сопротивление при  ,
, 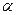 – температурный коэффициент сопротивления данного вещества (
– температурный коэффициент сопротивления данного вещества ( ):
): .
.
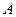 и вольтметра
и вольтметра  (рис. 1) непосредственно силы тока
(рис. 1) непосредственно силы тока  , протекающего через неизвестное сопротивление, и падения напряжения на нем
, протекающего через неизвестное сопротивление, и падения напряжения на нем  .
.
 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
 .
.
 узлов цепи. Однако независимыми являются только
узлов цепи. Однако независимыми являются только  уравнений, т.к.
уравнений, т.к.  Рис. 3
Рис. 3
 ,
,  и
и  . Условно выберем их направление, как показано на рисунке. Поскольку в схеме имеется два узла,
. Условно выберем их направление, как показано на рисунке. Поскольку в схеме имеется два узла, 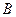 , по первому правилу Кирхгофа следует записать только одно уравнение. Так, для узла
, по первому правилу Кирхгофа следует записать только одно уравнение. Так, для узла  .
.
 .
.
 отмечено стрелками вокруг римских цифр). Правила знаков заключаются в следующем. Если направление обхода контура совпадает с направлением тока на участке цепи, падение напряжения на этом участке будем считать положительным, если нет – отрицательным. Если ток на участке цепи, содержащей ЭДС, совпадает с направлением тока внутри самого источника (ток внутри источника всегда направлен от минуса к плюсу), то ЭДС запишется со знаком "+", если нет – со знаком "–".
отмечено стрелками вокруг римских цифр). Правила знаков заключаются в следующем. Если направление обхода контура совпадает с направлением тока на участке цепи, падение напряжения на этом участке будем считать положительным, если нет – отрицательным. Если ток на участке цепи, содержащей ЭДС, совпадает с направлением тока внутри самого источника (ток внутри источника всегда направлен от минуса к плюсу), то ЭДС запишется со знаком "+", если нет – со знаком "–". ,
,
 .
.
 Рис.4
Рис.4
 (рис. 4), составленный из сопротивлений
(рис. 4), составленный из сопротивлений  ,
, 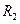 ,
,  и
и 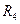 , соединенных между собой проводниками. В одну из диагоналей схемы через ключ
, соединенных между собой проводниками. В одну из диагоналей схемы через ключ  подключается источник тока с ЭДС
подключается источник тока с ЭДС  и внутренним сопротивлением
и внутренним сопротивлением  . В другую диагональ включается чувствительный нуль-гальванометр
. В другую диагональ включается чувствительный нуль-гальванометр 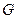 с сопротивлением
с сопротивлением  .
. ) моста (в силу его малости сопротивлением
) моста (в силу его малости сопротивлением  ,
,
 ,
,
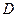 :
:  ,
,
 :
:  ,
,
 :
:  ,
,
 :
: 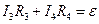 .
.
 , мост сопротивлений называется уравновешенным. При этом система (8) упрощается, и для нахождения неизвестного сопротивления достаточно уравнений:
, мост сопротивлений называется уравновешенным. При этом система (8) упрощается, и для нахождения неизвестного сопротивления достаточно уравнений: ,
,
 ,
,
 ,
,
 .
.
 .
.
 ,
,  , то в отсутствие тока в цепи гальванометра неизвестное сопротивление
, то в отсутствие тока в цепи гальванометра неизвестное сопротивление  можно определить по формуле:
можно определить по формуле: .
.
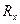 в работе используется резистор, роль сопротивлений
в работе используется резистор, роль сопротивлений 


