Определение коэффициента самоиндукции катушки
Принадлежности: исследуемая катушка, сердечник, вольтметр, амперметр, реостат, источник переменного тока. Краткая теория. Опыты Фарадея показали, что если проводник при своем движении пересекает магнитные силовые линии, на его концах наводится (индуктируется) электродвижущая сила (ЭДС), и если такой проводник замкнуть, то в нем потечет индукционный ток. Индукционный ток всегда направлен против вызвавшего его тока, препятствуя изменению последнего. Основной закон электромагнитной индукции имеет вид:
где В случае, когда таким проводником является катушка индуктивности, при изменении силы тока в катушке возникает ЭДС самоиндукции, величина которой пропорциональна изменению силы тока в единицу времени:
Здесь Индуктивность зависит от формы, размеров проводника и от магнитной проницаемости окружающей проводник среды. Единицей измерения индуктивности служит Генри (Гн): индуктивностью в 1 Гн обладает такой проводник, в котором изменение силы тока со скоростью в 1 А/с вызывает ЭДС самоиндукции в 1 В. У линейных проводников коэффициент самоиндукции мал, большими коэффициентами обладают катушки индуктивности (устройство, состоящее из большого числа витков проволоки). Сопротивление проволоки постоянному току равно Если в цепь переменного тока включен конденсатор Рассмотрим цепь, состоящую из последовательно соединенных элементов: сопротивления По второму правилу Кирхгофа:
где Дифференцируя уравнение (1) по времени и учитывая, что
Разделив это уравнение на
Здесь
Решение[1] неоднородного уравнения (2) сводится к решению однородного плюс решение любого частного, удовлетворяющего условиям задачи, а для установившихся колебаний практически равно частному. Частное решение уравнения (2) можно искать в виде
где Найти производные
Из векторной диаграммы легко найти амплитудное значение падения напряжения, приложенного к точкам
Отсюда можно найти амплитудное значение силы тока:
Разность фаз между током и напряжением
Уравнение (6) представляет собой закон Ома для переменных токов. При этом величина
называется полным сопротивлением цепи. Если цепь содержит только конденсатор (т.е.
которое обратно пропорционально электрической емкости Если в цепи имеется только катушка индуктивности (
Зависимость индуктивного сопротивления от частоты иная. Индуктивное сопротивление равно нулю в случае постоянного тока, Следует отметить, что решение дифференциального уравнения (2) совпадает с решением уравнения для механических колебаний. Сопоставление решений дает возможность заключить, что величина В выражении (6) фигурируют амплитудные значения силы тока Мощность, выделенная в цепи переменного тока за один период, равна:
Таким образом,
В работе для определения коэффициента самоиндукции катушки используется электрическая схема, состоящая из активного и индуктивного сопротивлений (рис. 3). В этом случае, как следует из выражений (6) и (7),
где полное сопротивление цепи
Коэффициент самоиндукции катушки
Видно, что для определения
|

 ,
,
 – скорость изменения магнитного потока относительно проводника.
– скорость изменения магнитного потока относительно проводника.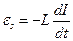 .
.
 – коэффициент самоиндукции или индуктивность.
– коэффициент самоиндукции или индуктивность.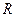 и называется активным. Если такую катушку включить в цепь переменного тока, то в ней возникает ЭДС самоиндукции и индукционный ток, который препятствует изменению приложенного к катушке напряжения. Это приводит к изменению сопротивления катушки: по величине оно становится больше активного; дополнительное сопротивление называется индуктивным
и называется активным. Если такую катушку включить в цепь переменного тока, то в ней возникает ЭДС самоиндукции и индукционный ток, который препятствует изменению приложенного к катушке напряжения. Это приводит к изменению сопротивления катушки: по величине оно становится больше активного; дополнительное сопротивление называется индуктивным  .
.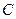 , то вследствие его перезарядки возникает емкостное сопротивление
, то вследствие его перезарядки возникает емкостное сопротивление 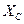 . Оба сопротивления
. Оба сопротивления  и
и  (рис.1).
(рис.1). ,
,
 – падение напряжения на активном сопротивлении катушки,
– падение напряжения на активном сопротивлении катушки, 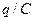 – напряжение на обкладках конденсатора; правая часть уравнения состоит из напряжения источника тока
– напряжение на обкладках конденсатора; правая часть уравнения состоит из напряжения источника тока  и ЭДС самоиндукции.
и ЭДС самоиндукции.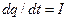 , получим:
, получим: .
.
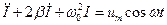 .
.
 – коэффициент затухания,
– коэффициент затухания,  – собственная частота контура,
– собственная частота контура,  .
. Рис. 1
Рис. 1
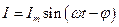 ,
,
 – разность фаз между силой тока и напряжением.
– разность фаз между силой тока и напряжением. ,
, 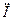 , подставив их значения и учитывая условие (3), решить уравнение (2). Можно использовать метод векторных диаграмм. Через все элементы схемы (рис. 1) течет один и тот же ток, поэтому на векторной диаграмме выберем направление оси токов
, подставив их значения и учитывая условие (3), решить уравнение (2). Можно использовать метод векторных диаграмм. Через все элементы схемы (рис. 1) течет один и тот же ток, поэтому на векторной диаграмме выберем направление оси токов  (рис. 2) и отложим амплитудные значения напряжений, учитывая фазовые соотношения между током и напряжениями. Поскольку падение напряжения на сопротивлении
(рис. 2) и отложим амплитудные значения напряжений, учитывая фазовые соотношения между током и напряжениями. Поскольку падение напряжения на сопротивлении 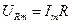 будет совпадать с током
будет совпадать с током 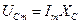 и
и 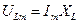 направлены в противоположные друг относительно друга стороны, т.к. по фазе напряжение на конденсаторе отстает от тока на угол
направлены в противоположные друг относительно друга стороны, т.к. по фазе напряжение на конденсаторе отстает от тока на угол 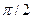 , а на катушке индуктивности – опережает на
, а на катушке индуктивности – опережает на 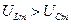 .
.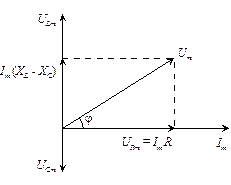 Рис. 2
Рис. 2
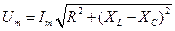 .
.
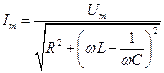 .
.
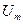 находится по тангенсу угла вектора
находится по тангенсу угла вектора  .
.
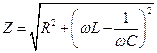
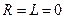 ), полное сопротивление цепи определяется величиной емкостного сопротивления
), полное сопротивление цепи определяется величиной емкостного сопротивления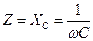 ,
,
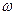 : при постоянном значении
: при постоянном значении 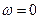 до нуля при
до нуля при 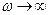 .
.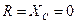 ), полное сопротивление равно индуктивному
), полное сопротивление равно индуктивному .
.
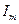 и напряжения
и напряжения  и
и 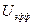 . Эффективные значения можно найти из мощности, выделяемой в цепи переменного тока.
. Эффективные значения можно найти из мощности, выделяемой в цепи переменного тока.
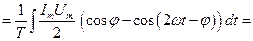

 и
и 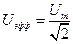 .
.
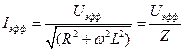 ,
,
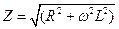 .
.
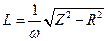 .
.
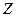 , т.к. циклическая частота переменного тока
, т.к. циклическая частота переменного тока 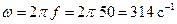 ) и сопротивление
) и сопротивление 


