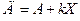Вычисление корреляционного отношения
Таким же способном определяем корреляционные отношения грубых ошибок χ по полетам у, ранжируя выборку по у и определяем ηу/х. Для оценки достоверности полученных величин используем формулу и по специальной таблице [52] находим значение Р= 99,9%.
Вычисление корреляционного отношения на больших выборках после предварительного заполнения корреляционной решетки можно производить по способу произведений, способу условных средних и способу суммирования [141]. Регрессионный анализ. Описанные показатели корреляции позволяют измерять степень связи, направление и форму существующей между ними зависимости. Однако они не дают информации о том, насколько в среднем может измениться в ту или другую сторону один из признаков при изменении другого. Такая информация представляет большой практический интерес для разработки методик психологического отбора, а также изучения влияния специальных методов подготовки на успешность профессионального обучения. Функция, позволяющая по величине одного признака (х) находить средние (ожидаемые) значения другого признака ( Важную роль в регрессионном анализе играет коэффициент регрессии (R), являющийся не только параметром уравнения, но и мерой регрессии у по x и x по у. Показатели его величины (n) характеризуют зависимость между переменными x и у по их абсолютным значениям, а показатели корреляции – величины относительные и измеряют тесноту связи между признаками в долях единицы. Коэффициент регрессии характеризует только линейную связь, при которой увеличения (уменьшения) одной переменной – у – пропорциональны увеличениям другой – х, и в зависимости от направления связь либо положительна, либо отрицательна. По знач ениям R легко определяется коэффициент корреляции Коэффициент регрессии позволяет рассчитать, насколько в среднем изменится признак при изменении на единицу меры другого связанного с ним признака. Он рассчитывается по коэффициентам корреляции и средним квадратическим отклонениям сопряженных видов по следующим формулам:
По формулам Ry/x. определяется среднее (ожидаемое) значение у при изменении на единицу меры х, а по формулам Rx/y находят среднюю величину χ при изменении на единицу меры признака у. Имея возможность легко менять условия проведения эксперимента по методике у и быстро оценивать полученные результаты, мы можем установить необходимые или оптимальные условия для другой методики х – более сложной и трудоемкой. Зная интеркорреляционные связи между методиками «батареи» тестов и проводя регрессионный анализ, можно добиться оптимальных и наиболее целесообразных условий их проведения и соответственно повысить прогно-стичность «батареи» в целом. Например, коэффициент корреляции между результатами обследования по методике y(время – с.) и x(количество ошибок) равен +0,25; σy = 27, σχ = 5. Подставляя значения в формулу, находим Ry/χ = 1,35 и Rx/y = 0,995. Это означает, что увеличение времени выполнения на 1 сек соответствует увеличению количества ошибок в среднем на 0,05 ошибок, а увеличение на одну ошибку при выполнении задания соответствует увеличению времени чтения таблицы на 1,35 с. Если сравнивать время чтения и количество ошибок по отношениям между средними арифметическими величинами этих признаков ( Достоверность коэффициента регрессии, как и любого другого выборочного показателя, оценивается по критерию Стьюдента с числом степеней свободы К = Ν-2. В обоих случаях ty/x и tx/y коэффициенты регрессии достоверны на 99,9%-ном уровне. Для прогнозирования успешности обучения и реальной деятельности (по результатам психологического обследования) может быть использован аппарат регрессионного и последовательно-дискриминантного анализа. А.Н. Лебедев разработал компьютерные программы факторного, кластерного и регрессионного анализа, которые использовались для распознавания внешнего критерия эффективности службы в системе органов внутренних дел [1961. Мерой связи между внешним критерием (например, фактором «профессионализм») и тестовым показателем служит коэффициент линейной корреляции по Пирсону. Коэффициент принимает значения от –1 до +1. Показатели связаны положительно, если с ростом одного из них возрастает и второй, и, наоборот, при росте одного и уменьшении другого. Коэффициенты корреляции рассчитываются для выборки в целом. Однако интерес представляет конкретный человек, у которого по показателям психодиагностических измерений можно было бы предсказать профессиональную успешность. Для этого используется техника регрессионного анализа. В простейшем случае, если обозначить буквой «Д» прогнозируемую оценку профессиональной успешности конкретного человека, а «X» – его тестовый показатель, то прогноз можно определить по формуле:
где r– коэффициент корреляции. От относительных величин (нормированных) легко перейти к абсолютным. В этом случае формула регрессии принимает вид:
где Д и X– нормированные показатели; А – свободный член; к – коэффициент при аргументе, то есть тестовом показателе. Полностью поведение человека непредсказуемо, и коэффициент корреляции между внешним (рабочим) поведением и результатами отдельных тестовых измерений, как правило, составляет 0,2–0,3. Однако множество разных тестовых по казателей, взятых в совокупности, связаны с прогнозируемым поведенческим качеством сильнее. Происходит совокупное усиление возможностей в задаче распознавания внешнего «образа». Для прогноза в этом случае используется уравнение множественной регрессии типа:
где Д– прогнозируемая поведенческая величина (например, уровень «профессионализма»), R, m, i, q– коэффициенты уравнения, полученные ранее на большой выборке испытуемых; X1 X2, Х3... Хn – показатели тестовых измерений. Для получения коэффициентов диагностических уравнений множественной регрессии иногда используют не всю выборку, а только полярные группы, то есть самых успешных профессионалов и тех, от которых целесообразно избавиться. Разработанный методический подход, по мнению Б. Г. Бовина, имеет свои преимущества и недостатки [196]. Положительными качествами являются, в частности, быстрота расчета и эффективность оценивания информативности применяемых методов. Одновременно можно использовать практически любое количество показателей, из которых автоматизированная процедура позволяет сделать выбор тех, которые имеют отношение к распознаванию заданного «образа». Заданным «образом» может быть любой внешний критерий: наиболее и наименее профессионально успешные сотрудники, студенты с разным уровнем академической успеваемости, виновники аварийных ситуаций и т. п. Другим преимуществом является достаточно полная картина статистических характеристик, получаемых на промежуточном этапе, которые позволяют исследовать многочисленные связи между используемыми параметрами. Различные психодиагностические методы могут сравниваться по тому вкладу, который они вносят в распознавание заданного «образа». В этом случае можно проверять валидность любых тестов, использование которых дает цифровой показатель. Последнее преимущество имеет и свой недостаток – происходит определенное «выхолащивание» качественного, содержательного аспекта диагностики. Другим недостатком является нестабильность получаемых моделей распознавания. Каждая новая выборка дает новую модель распознавания неизменного внешнего критерия. В эту модель могут войти другие показатели, ранее отвергнутые в ходе регрессионной процедуры. Это создает ощущение определенной ненадежности полученных результатов. Однако эта неопределенность объясняется тем, что различные показатели обусловлены одним и тем же фактором, то есть несмотря на многовариатив-ность моделей, содержательная сущность их сохраняется.
|

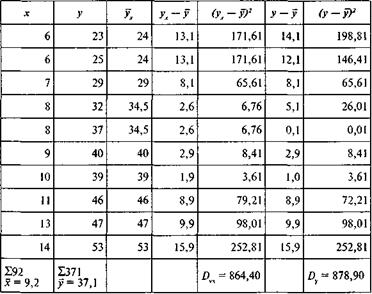
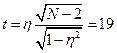
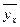 ), связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного.
), связанного с x корреляционно, называется регрессией, а статистический анализ регрессии получил название регрессионного. . Зависимость между R и r позволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по - известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными.
. Зависимость между R и r позволяет контролировать правильность расчета этих показателей, а также находить неизвестную величину одного из них по - известной другой. Кроме того, при помощи регрессионного анализа можно исследовать корреляционную зависимость между признаками при малых выборках, но при этом необходимо помнить, что полученные коэффициенты могут оказаться несколько завышенными. ;
; 
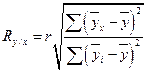 ;
; 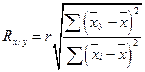
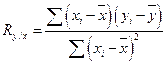 ;
; 
 = 242,
= 242,  = 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку– 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии у по x и x по у. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.
= 41), то получается, что на 1 с увеличения приходится 0,17 ошибки, а на 1 ошибку– 5,9 с. Как видно из сравнения, отношения средних арифметических величин дают более высокие показатели, чем значения коэффициента регрессии. Причина такого расхождения заключается в том, что отношение не учитывает корреляционную зависимость между признаками, поэтому и не может служить показателем регрессии у по x и x по у. Чем меньше коэффициент корреляции между изучаемыми признаками, тем больше расхождение будет между отношениями по средним величинам и коэффициенту регрессии.