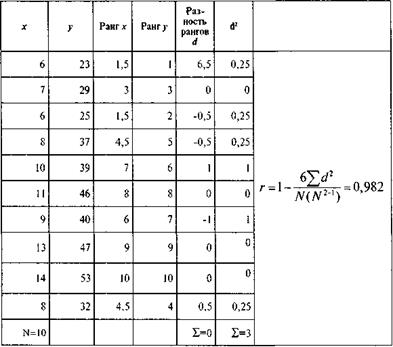
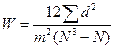Расчет показателя корреляции рангов
При изучении корреляционной зависимости между критериями, выраженными в баллах или классовых вариантах и при большом количестве сопоставляемых пар, целесообразней г вычислять по способу сумм [141] с использованием корреляционной решетки и формулы
где Spaxay – сумма произведений частот корреляционной решетки (Рхy) на соответствующие порядковые номера классов (баллов); S– сумма первого полного ряда накопленных частот, получаемого кумуляцией частот каждого ряда в направлении, обратном порядковой нумерации классов; σχ и σy - средние квадратические отклонения рядов; Ν– общее число парных наблюдений. Изучая корреляционную связь между двумя признаками χ и у, необходимо помнить о возможности существования зависимости или влияния на них других варьирующих признаков. Поэтому наряду с изучением парных корреляций возникает задача измерения множественных связей между варьирующими признаками индивидуальных психофизиологических особенностей организма и критериями успешности обучения. Для решения этой задачи необходимо воспользоваться коэффициентом общей или совокупной корреляции и частными или парциальными коэффициентами корреляции. Совокупный коэффициент корреляции между варьирующими признаками х,у и z вычисляется по следующей формуле:
где r хy, rхz и rxz– парные коэффициенты линейной корреляции между признаками χ и у, χ и z, у и z. На практике чаще применяется парциальный коэффициент корреляции, измеряющий связь между двумя варьирующими признаками χ и у при постоянном значении третьего – z – учитываемого признака, который может иметь или имеет связь с первыми двумя. Так, парциальный коэффициент между χ и у при исключительном влиянии на эту связь, составляет
Соответственно рассчитываются коэффициенты парциальной корреляции между χ и z при влиянии y–rxz(y); у к z – при влиянии х–ryz(x). Как видно из приведенных формул, расчет значений со вокупного и парциальных коэффициентов корреляций производится на основе парных коэффициентов корреляций. В некоторых случаях возникает необходимость изучения связи между несколькими внешними критериями, даваемыми разными экспертами (независимые характеристики, ранжирование и др), и ее достоверности. Например, для обеспечения объективности выведения оценки летных способностей курсантов по 9-балльной шкале по мнению четырех экспертов А, Б, В, Г из летно-инструкторского состава (командир и его заместители) необходимо определить степень совпадения их мнений в отношении одних и тех же курсантов. Для этой цели используется показатель корреляции рангов для суммарной ранжировки – коэффициент конкордации
где Σd2 – сумма квадратов отклонений индивидуальных сумм рангов от средней индивидуальной суммы рангов; т – число сравниваемых ранжированных рядов; Ν– численность выборки, W показывает степень согласия ранжированных рядов, и его значения могут колебаться от 0 до 1 (табл. 9). В данном примере он достаточно высок (W= 0,91) и свидетельствует о единстве мнений внешних экспертов по оценке летных способностей курсантов. В ряде случаев, когда критерии профессионально-психологической пригодности и успешности обучения не распределяются в вариационный ряд, корреляция между ними устанавливается по наличию нескольких качественных признаков в связи с качественными признаками обучения. Корреляция между качественными признаками, группируемыми в 4-клеточную корреляционную решетку, определяется с помощью коэффициента ассоциации (ra) Дж. Юла – тетрахорического показателя связи. Когда изучается корреляционная зависимость между несколькими качественными признаками, группируемыми в многоклеточные таблицы, используется коэффициент взаимной сопряженности (К) – полихорический показатель связи. Таблица 9
|