Theoretical part. The main characteristic of a magnetic field in a medium is the magnetic induction which is determined by the force acting on an element of a conductor with a
The main characteristic of a magnetic field in a medium is the magnetic induction
where I is a current; Currents of any origin are sources of a magnetic field. Closed microscopic currents related to, for example, motion of electrons in atoms are always presented in a medium. Hence the total magnetic field in a medium
where For a homogeneous isotropic medium (nonferromagnetic), relation between magnetic polarization and intensity is considered to be linear:
The proportionality coefficient
where Magnetic intensity at an arbitrary point is determined by a current distribution in conductors. If currents flow along wires, intensity at distances much more than a transverse size of the wires can be found by using the Biot-Savart-Laplace formula
In this formula, Using formula (13.5), it is easy to determine magnetic intensity on an axis of a circular turn with current (of magnitude I and radius R):
where l is the distance from the point where intensity has to be found to the center of the turn.
|

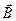 which is determined by the force acting on an element of a conductor with a current:
which is determined by the force acting on an element of a conductor with a current: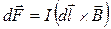 , (13.1)
, (13.1)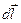 is the vector which magnitude is equal to length of a conductor section and it’s direction coincides with a current direction. The boldface multiplication sign denotes the vector product.
is the vector which magnitude is equal to length of a conductor section and it’s direction coincides with a current direction. The boldface multiplication sign denotes the vector product.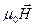 and one produced by microscopic currents in a magnetized medium (a magnetic)
and one produced by microscopic currents in a magnetized medium (a magnetic) 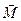 :
: , (13.2)
, (13.2)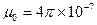 H/m.
H/m. 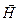 is called the intensity of a magnetic field,
is called the intensity of a magnetic field,  . (13.3)
. (13.3)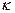 is called the magnetic susceptibility. After substitution of (13.3) into (13.2), we obtain the relationship between induction and intensity
is called the magnetic susceptibility. After substitution of (13.3) into (13.2), we obtain the relationship between induction and intensity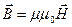 , (13.4)
, (13.4)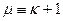 is called the magnetic permeability of the medium. In contrast to the dielectric permeability, the magnetic permeability can be either much or less than 1. Typical values of susceptibility for nonferromagnetic substances are 0.38×10-6 (air), -26×10-6 (silver), 300×10-6 (platinum).
is called the magnetic permeability of the medium. In contrast to the dielectric permeability, the magnetic permeability can be either much or less than 1. Typical values of susceptibility for nonferromagnetic substances are 0.38×10-6 (air), -26×10-6 (silver), 300×10-6 (platinum).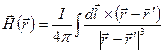 . (13.5)
. (13.5)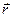 identifies position of the point where intensity has to be found;
identifies position of the point where intensity has to be found; 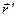 is the radius-vector of the wire element
is the radius-vector of the wire element 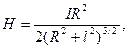 (13.6)
(13.6)