Силовими характеристиками магнітного поля є індукція 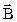 і напруженість
і напруженість  . Індукція визначається за законом Ампера, який у 1820 р. встановив, що сила
. Індукція визначається за законом Ампера, який у 1820 р. встановив, що сила  , яка діє на провідник із струмом I, прямопропорційна величині струму, довжині провідника
, яка діє на провідник із струмом I, прямопропорційна величині струму, довжині провідника 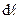 і синусу кута
і синусу кута 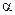 між провідником та напрямком індукції магнітного поля (рис.2)
між провідником та напрямком індукції магнітного поля (рис.2)
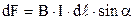 . (12.1)
. (12.1)
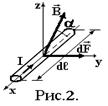 Сила максимальна, коли α = 90о, тобто коли провідник із струмом перпендикулярний до магнітного поля. Тоді індукція
Сила максимальна, коли α = 90о, тобто коли провідник із струмом перпендикулярний до магнітного поля. Тоді індукція
 (12.2)
(12.2)
чисельно дорівнює силі, що діє на 1м прямолінійного провідника із струмом в 1А, який перпендикулярний до магнітного поля. Вимірюється індукція в системі СІ в теслах (Тл).
Якщо довжину провідника розглядати як вектор, напрямок якого співпадає із напрямком струму, то закон Ампера (12.1) у векторній формі має вид
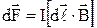 . (12.3)
. (12.3)
Напрямок сили Ампера можна визначити за правилом лівої руки: якщо ліву руку розмістити так, щоб силові лінії входили в долоню, чотири витягнутих пальці направити по струмові, то відігнутий великий палець вкаже напрямок сили.
Силова характеристика магнітного поля, яка не залежить від магнітних властивостей середовища є напруженість
 . (12.4)
. (12.4)
тут: μ – відносна магнітна проникність середовища, показує у скільки разів індукція поля в середовищі більша, ніж у вакуумі; μо = 4∙π∙10-7 Гн/м – магнітна стала.
 Закон трьох французьких вчених Біо(1774-1862), Савара (1791-1841) і Лапласа(1749-1827) – це експериментальний закон, який визначає напруженість
Закон трьох французьких вчених Біо(1774-1862), Савара (1791-1841) і Лапласа(1749-1827) – це експериментальний закон, який визначає напруженість 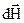 магнітного поля, створеного елементом провідника довжиною
магнітного поля, створеного елементом провідника довжиною  із струмом I в точці, віддаленій від цього елементу на відстань
із струмом I в точці, віддаленій від цього елементу на відстань  (рис.3)
(рис.3)
 , (12.5)
, (12.5)
або в скалярній формі

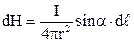 . (12.6)
. (12.6)
 Знайдемо напруженість магнітного поля на осі колового провідника радіусом R, по якому тече струм І. Положення точки задамо висотою h від центра кола (рис.4). Спочатку визначимо напрямок вектора
Знайдемо напруженість магнітного поля на осі колового провідника радіусом R, по якому тече струм І. Положення точки задамо висотою h від центра кола (рис.4). Спочатку визначимо напрямок вектора  . Для цього виберемо два однакових діаметрально протилежних елементи провідника
. Для цього виберемо два однакових діаметрально протилежних елементи провідника  . Вони створюють у даній точці вектори напруженості
. Вони створюють у даній точці вектори напруженості 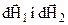 , які
, які  перпендикулярні до відповідних радіус-векторів і однакові за величиною. Спроектуємо ці вектори напруженостей на осі x і y. З рисунка видно, що
перпендикулярні до відповідних радіус-векторів і однакові за величиною. Спроектуємо ці вектори напруженостей на осі x і y. З рисунка видно, що 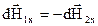 , тобто попарно компенсуються. Проекції на вісь у направлені паралельно, тому будемо додавати їх алгебраїчно. Таким чином результуючий вектор направлений вздовж осі кільця у відповідності з правилом правого гвинта: якщо обертати гвинт у напрямку струму, його поступальний рух вздовж осі вказує напрямок вектора напруженості.
, тобто попарно компенсуються. Проекції на вісь у направлені паралельно, тому будемо додавати їх алгебраїчно. Таким чином результуючий вектор направлений вздовж осі кільця у відповідності з правилом правого гвинта: якщо обертати гвинт у напрямку струму, його поступальний рух вздовж осі вказує напрямок вектора напруженості.
За принципом суперпозиції напруженість магнітного поля будь-якого провідника зі струмом дорівнює векторній сумі напруженостей, створених у даній точці кожним елементом  провідника. Для цього необхідно розрахувати криволінійний інтеграл
провідника. Для цього необхідно розрахувати криволінійний інтеграл
 . (12.7)
. (12.7)
Враховуючи (12.6), маємо
. 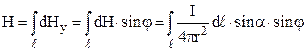
Кут α між векторами  та
та  дорівнює 90о;
дорівнює 90о;  ;
;  .
.

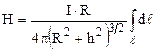 .
.
Так як  є довжина кола, одержуємо
є довжина кола, одержуємо
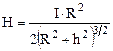 . (12.8)
. (12.8)
В центрі колового струму при h = 0 отримуємо
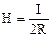 . (12.9)
. (12.9)

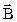 і напруженість
і напруженість  . Індукція визначається за законом Ампера, який у 1820 р. встановив, що сила
. Індукція визначається за законом Ампера, який у 1820 р. встановив, що сила  , яка діє на провідник із струмом I, прямопропорційна величині струму, довжині провідника
, яка діє на провідник із струмом I, прямопропорційна величині струму, довжині провідника 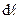 і синусу кута
і синусу кута 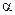 між провідником та напрямком індукції магнітного поля (рис.2)
між провідником та напрямком індукції магнітного поля (рис.2)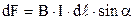 . (12.1)
. (12.1) Сила максимальна, коли α = 90о, тобто коли провідник із струмом перпендикулярний до магнітного поля. Тоді індукція
Сила максимальна, коли α = 90о, тобто коли провідник із струмом перпендикулярний до магнітного поля. Тоді індукція (12.2)
(12.2)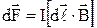 . (12.3)
. (12.3) . (12.4)
. (12.4) Закон трьох французьких вчених Біо(1774-1862), Савара (1791-1841) і Лапласа(1749-1827) – це експериментальний закон, який визначає напруженість
Закон трьох французьких вчених Біо(1774-1862), Савара (1791-1841) і Лапласа(1749-1827) – це експериментальний закон, який визначає напруженість 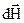 магнітного поля, створеного елементом провідника довжиною
магнітного поля, створеного елементом провідника довжиною  із струмом I в точці, віддаленій від цього елементу на відстань
із струмом I в точці, віддаленій від цього елементу на відстань  (рис.3)
(рис.3) , (12.5)
, (12.5)
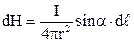 . (12.6)
. (12.6) Знайдемо напруженість магнітного поля на осі колового провідника радіусом R, по якому тече струм І. Положення точки задамо висотою h від центра кола (рис.4). Спочатку визначимо напрямок вектора
Знайдемо напруженість магнітного поля на осі колового провідника радіусом R, по якому тече струм І. Положення точки задамо висотою h від центра кола (рис.4). Спочатку визначимо напрямок вектора  . Для цього виберемо два однакових діаметрально протилежних елементи провідника
. Для цього виберемо два однакових діаметрально протилежних елементи провідника  . Вони створюють у даній точці вектори напруженості
. Вони створюють у даній точці вектори напруженості 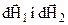 , які
, які  перпендикулярні до відповідних радіус-векторів і однакові за величиною. Спроектуємо ці вектори напруженостей на осі x і y. З рисунка видно, що
перпендикулярні до відповідних радіус-векторів і однакові за величиною. Спроектуємо ці вектори напруженостей на осі x і y. З рисунка видно, що 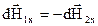 , тобто попарно компенсуються. Проекції на вісь у направлені паралельно, тому будемо додавати їх алгебраїчно. Таким чином результуючий вектор направлений вздовж осі кільця у відповідності з правилом правого гвинта: якщо обертати гвинт у напрямку струму, його поступальний рух вздовж осі вказує напрямок вектора напруженості.
, тобто попарно компенсуються. Проекції на вісь у направлені паралельно, тому будемо додавати їх алгебраїчно. Таким чином результуючий вектор направлений вздовж осі кільця у відповідності з правилом правого гвинта: якщо обертати гвинт у напрямку струму, його поступальний рух вздовж осі вказує напрямок вектора напруженості. провідника. Для цього необхідно розрахувати криволінійний інтеграл
провідника. Для цього необхідно розрахувати криволінійний інтеграл . (12.7)
. (12.7)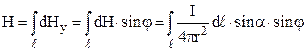
 та
та  дорівнює 90о;
дорівнює 90о;  ;
;  .
.
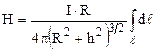 .
. є довжина кола, одержуємо
є довжина кола, одержуємо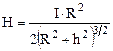 . (12.8)
. (12.8)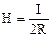 . (12.9)
. (12.9)


