Факторы накопления
Поле фотонного излучения в реальных задачах определяется не только не рассеянным излучением источника, но и рассеянными фотонами, которые испытали однократное или многократное (2 и более) взаимодействий в воздухе или материале поглотителя. Кроме этого, в детектор попадает также вторичное излучение: аннигиляционное, характеристическое, тормозное. Геометрию, при которой детектор регистрирует не рассеянное (первичное), рассеянное излучения, а также вторичное излучение, называют геометрией широкогопучка или "плохой" геометрией (рис.2). Выражения для ослабления мононаправленного параллельного пучка очень удобны для расчета ослабления излучения в веществе. Чтобы сохранить простоту записи и при этом учесть рассеянное излучение поступают следующим образом. Рассеянное в среде излучение источника и вторичное излучение учитывают введением в закон ослабления в геометрии узкого пучка сомножителя - фактора накопленияфотонного излучения
Из этой формулы следует, что
Рис. 2. Схема эксперимента в геометрии широкого пучка: S – источник, К – коллиматор, П – поглотитель, Д – детектор
Можно сказать, что фактор накопления (ФН) равен отношению показания детектора при измерении в геометрии широкого пучка к показанию детектора при измерении в геометрии узкого пучка. ФН зависит от многих условий задачи: от того, какая характеристика поля излучения регистрируется, от геометрии, от спектра и углового распределения источника, от толщины и материала защиты, от взаимного расположения источника и детектора. В зависимости от регистрируемых характеристик поля излучения различают следующие ФН (определения даются для первичного излучения с энергией Е0). Числовой ФН (для плотности потока фотонов j): Вч(х) = ò j(Е,x) dE / j(Е0,x) Энергетический ФН(для интенсивности фотонов): Вэ(х) = ò j(Е,x)E dE / (j(Е0,x)×Е0) Дозовый ФН(для поглощённой дозы в воздухе, для экспозиционной дозы): ВD(х) = ò j(Е,x) E аmв(E) dE / (j(Е0,x) Е0 аm в (Е0)), здесь аmв(Е) – коэффициент поглощения энергии фотонов в воздухе. ФН поглощённой энергии (для поглощённой в среде энергии): Вп(х) = ò j(Е,x) E аmср(E) dE / (j(Е0,x) Е0 аmср (Е0)), здес аmср(Е) – коэффициент поглощения энергии в данной среде. Отметим, что дозовый ФН равен ФН поглощённой энергии в воздухе. Удобство применения ФН заключается также в том, что он изменяется достаточно плавно в зависимости от x, Е0 и Z вещества и можно проводить достаточно точную интерполяцию ФН по ограниченному числу расчётных и экспериментальных данных. Наиболее часто используют следующие аппроксимационные формулы: Формула Бергера:В(mx) = 1+a ×;mx×exp(b×mx) (mx < 10) Коэффициенты а и bприводятся в специальных таблицах. Формула ТейлораВ(Е0, mx, Z) = А1exp(-a1×mx) + (1-А1) exp(-a2×mx). Коэффициенты А1, a1 , a2 имеются в таблицах в литературе.
Основные закономерности поведения фактора накопления: · ФН монотонно возрастает с увеличением толщины вещества, так как увеличивается доля фотонов, испытавших рассеяние. Для высоких энергий и материалов с небольшими Z скорость возрастания ФН почти линейная от толщины. Для элементов с большим Z ФН растет медленнее за счет большего фотопоглощения. · ФН возрастает при увеличении изотропии источника, при этом для постоянного расстояния между источником и детектором справедливо следующее соотношение: В¥ > В бар > В огр, т.е. наибольший ФН в бесконечной среде. · ФН при одной энергии фотонов больше в веществах с меньшим Z, где меньше сечение фотоэффекта, который приводит к поглощению излучения; при большой энергии фотонов он больше в веществах с большим · ФН зависит от поперечных размеров источника и возрастает с их увеличением.
В отдельных случаях на больших расстояниях от источника вклад рассеянного излучения в поле излучения является преобладающим и может в десятки-сотни раз превышать вклад от не рассеянного излучения.
|

 :
:
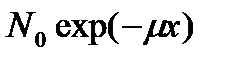 .
. за счёт интенсивной генерации вторичного излучения;
за счёт интенсивной генерации вторичного излучения;


