Ввод эллипсов
2.6.1. Построение эллипса с заданным центром, через две указанные точки
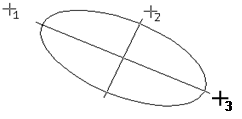
Для вызова команды активируйте пиктограмму Ввод эллипса. Введите центральную точку эллипса. Затем укажите две точки, лежащие на эллипсе или введите значения координат точек в полях Строки параметров объектов.
Рис. 2.26. Эллипс по центру и двум точкам
2.6.2. Построение эллипса с заданным центром, размерами полуосей и углом наклона полуоси
Команда ввод эллипса п озволяет начертить один или несколько произвольных эллипсов с заданным центром, полуосями и углом наклона полуоси.
Введите центральную точку эллипса. Затем укажите две точки, определяющие величину полуосей эллипса. Вы можете вводить значения координат точек, размеры и угол наклона полуосей в полях Строки параметров объектов.
Рис. 2.27. Эллипс по центру и размерам полуосей 2.6.3. Построение эллипса по диагонали габаритного прямоугольника
Для вызова команды активируйте пиктограмму Эллипс по диагонали габаритного прямоугольника. Укажите начальную и конечную точки, определяющие диагональ прямоугольника или задайте координаты точек и угол наклона сторон прямоугольника в соответствующих полях Строки параметров объектов.
Рис. 2.28. Эллипс по диагонали габаритного прямоугольника 2.6.4. Построение эллипса по центру и углу прямоугольника
Команда Эллипс по центру и углу габаритного прямоугольника позволяет начертить эллипс, задав положение центра и угловой точки ограничивающего прямоугольника.
Укажите центр габаритного прямоугольника, а затем его угловую точку или задайте координаты точек и угол наклона осей эллипса в соответствующих полях Строки параметров объектов.
Рис.2.29. Построение эллипса по центру и углу прямоугольника
2.6.5. Построение эллипса по центру, середине и углу параллелограмма
Команда Эллипс по центру, середине стороны и углу описанного параллелограмма позволяет начертить эллипс, задав положение центра, середины стороны и угловой точки описанного вокруг эллипса параллелограмма.
Последовательно укажите курсором центр эллипса, а затем середину стороны и угол описанного параллелограмма. Можно также задать координаты точек в соответствующих полях Строки параметров объектов.
Рис. 2.30. Построение эллипса по центру, середине стороны и углу параллелограмма
2.6.6. Построение эллипса по трем вершинам параллелограмма
Команда Эллипс по трем углам описанного параллелограмма п озволяет начертить эллипс, задав положение трех вершин описанного параллелограмма.
Последовательно укажите курсором три точки, определяющие параллелограмм. Можно также задать координаты точек в соответствующих полях Строки параметров объектов
Рис. 2.31. Построение эллипса по трем вершинам габаритного параллелограмма
|

 Команда Ввод эллипса позволяет начертить один или несколько произвольных эллипсов.
Команда Ввод эллипса позволяет начертить один или несколько произвольных эллипсов.
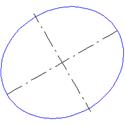

 Команда Эллипс по диагонали габаритного прямоугольника позволяет начертить эллипс, задав диагональ ограничивающего прямоугольника.
Команда Эллипс по диагонали габаритного прямоугольника позволяет начертить эллипс, задав диагональ ограничивающего прямоугольника.
 Для вызова команды активируйте пиктограмму Эллипс по центру и углу габаритного
Для вызова команды активируйте пиктограмму Эллипс по центру и углу габаритного 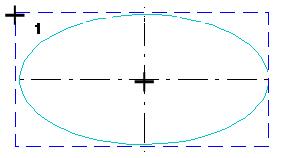
 Для вызова команды активизируйте пиктограмму Эллипс по центру, середине стороны и углу описанного параллелограмма.
Для вызова команды активизируйте пиктограмму Эллипс по центру, середине стороны и углу описанного параллелограмма.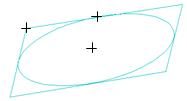
 Для вызова команды активируйте пиктограмму Эллипс по трем вершинам описанного параллелограмма.
Для вызова команды активируйте пиктограмму Эллипс по трем вершинам описанного параллелограмма.