Ввод дуг
2.5.1. Построение дуги с вводом центра и двух точек
Команда Дуга по центру и двум точкам позволяет начертить одну или несколько дуг.
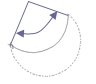
Дуга по центру и двум точкам. Введите центральную точку дуги. Затем задайте положение начальной и конечной точек дуги. Радиус дуги определяется по первой указанной точке.
Рис. 2.31. Дуга по центру и двум точкам
Можно построить несколько дуг, имеющих одинаковый центр и величину радиуса. Укажите точку центра. Введите нужное значение радиуса в поле Строки парков и зафиксируйте его, а затем нажмите кнопку Запомнить состояние. П оследовательно создавайте дуги, указывая их начальные и конечные точки.
2.5.2. Построение дуги с вводом центра, начального и конечного углов и точки на дуге
Дуга по центру и двум точкам. - указать точку центра дуги, зафиксировать ее курсором или задав координаты; - введите начальный угол дуги, нажмите <enter>; - введите конечный угол дуги, нажмите <enter>; - перемещайте курсор по полю чертежа;
- зафиксируйте положение дуги клавишей <enter>.
Рис. 2.32. Дуга по центру и начальному и конечному углу и точке на дуге
2.5.3. Построение дуги с вводом центра, начального и конечного углов, радиуса
Построить дугу в соответствии с п. 2.5.2, но ввести не точку на дуге, а задать значение радиуса на панели строки состояния.
2.5.4. Построение дуги с вводом центра, начального и конечного углов, радиуса и со сменой направления дуги
2.5.5. Построение дуги по трем точкам
Позволяет начертить дугу с указанными концами, проходящую через заданную точку.
Последовательно укажите точку, через которую должна пройти дуга, начало и конец дуги.
Рис.2.33. Построение дуги по трем точкампо трем точкам 2.5.6. Построение дуги, касательной к кривой
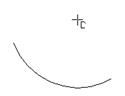
Команда Дуга, касательная к кривой позволяет начертить дугу, касательную к заданному объекту.
Укажите курсором кривую, которую должна касаться дуга. Затем последовательно введите точку, через которую должна пройти дуга, и конечную точку дуги. Можно также задать радиус дуги в соответствующем поле Строки параметров объектов. На экране будут показаны все варианты дуг.
Рис. 2.24. Дуги, касательные к отрезку
2.5.7. Построение дуги по двум точкам
Команда Дуги по двум точкам позволяет начертить дугу с концами в двух заданных точках. Укажите курсором или задайте координаты концов дуги. Если радиус явно не задавать, то будет построена дуга с радиусом, равным половине расстояния между указанными точками и углом раствора 180°.
2.5.8. Построение дуги по двум точкам и углу раствора
Команда позволяет начертить дугу с заданным углом раствора и заданными начальной и конечной точками дуги.
Введите значение угла раствора в Строке параметров объекта. Затем укажите точки начала и конца дуги.
Рис. 2.25. Дуга по двум точкам и углу раствора
|

 Для вызова команды активизируйте пиктограмму
Для вызова команды активизируйте пиктограмму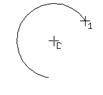
 Изменить направление дуги можно нажав кнопку Направление в Строке параметров объектов.
Изменить направление дуги можно нажав кнопку Направление в Строке параметров объектов.
 Построить дугу в соответствии с п. 2.5.2, но перед тем как зафиксировать ее, активировать пиктограмму Направление дуги.
Построить дугу в соответствии с п. 2.5.2, но перед тем как зафиксировать ее, активировать пиктограмму Направление дуги. Для вызова команды активизируйте пиктограмму Дуга потрем точкам
Для вызова команды активизируйте пиктограмму Дуга потрем точкам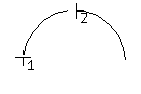
 Для вызова команды активируйте пиктограмму Дуга, касательная к кривой.
Для вызова команды активируйте пиктограмму Дуга, касательная к кривой.
 Для вызова команды активируйте пиктограмму Дуга по двум точкам и углу раствора.
Для вызова команды активируйте пиктограмму Дуга по двум точкам и углу раствора.