Ввод многоугольников
2.9.1. Построение прямоугольника по двум его вершинам
Для вызова команды активируйте пиктограмму Ввод прямоугольника на Инструментальной панели. Укажите первую, а затем вторую точки диагонали прямоугольника. Вы можете ввести значения координат вершин прямоугольника в полях Строки параметров объектов. Можно задать значения ширины и высоты прямоугольника в соответствующих полях Строки параметров.
Рис. 2.35. Построение прямоугольника по диагональным точкам
Построенный прямоугольник - это единый объект, а не набор отдельных отрезков. Он будет выделяться, редактироваться и удаляться целиком.
2.9.2. Построение прямоугольника по его центру и углу
Команда Прямоугольник по центру и углу Позволяет построить прямоугольник, указав его центр и угол.
Кнопка Прямоугольник по центру и углу Укажите центр прямоугольника, а затем его угол. Вы можете ввести значени я координат точек в полях Строки параметров объектов. Можно также задать значения ширины и высоты прямоугольника в соответствующих полях Строки параметров.
Рис. 2.36. Построение прямоугольника по центру и углу
2.9.3. Построение правильных многоугольников
Команда Многоугольник позволяет построить один или несколько правильных многоугольников.
Задайте число вершин многоугольника в поле Строки параметров объектов. Затем укажите точку центра базовой окружности и точку на этой окружности, определяющую многоугольник. Можно ввести координаты центра окружности, радиус, координаты точки на окружности, а также угол наклона многоугольника в полях Строки параметров. Для переключения варианта построения многоугольника (по вписанной или описанной окружности) используйте специальную кнопку в Строке параметров объектов. При переключении внешний вид этой:
Построенный многоугольник - это единый объект, а не набор отдельных отрезков. Он будет выделяться, редактироваться и удаляться целиком. Построение осей возможно только для многоугольников с четным количеством углов (шестиугольников, восьмиугольников и т.д.).
|

 Команда Ввод прямоугольника позволяет построить прямоугольник, указав концы его диагонали.
Команда Ввод прямоугольника позволяет построить прямоугольник, указав концы его диагонали.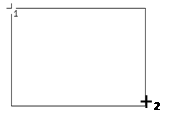
 Для вызова команды нажмите кнопку Прямоугольник по центру и углу.
Для вызова команды нажмите кнопку Прямоугольник по центру и углу.
 Для вызова команды активируйте пиктограмму Многоугольник.
Для вызова команды активируйте пиктограмму Многоугольник. по вписанной окружности
по вписанной окружности по описанной окружности.
по описанной окружности.
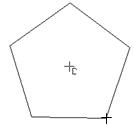
 Рис. 2.37. Пятигранник по вписанной и описанной окружности
Рис. 2.37. Пятигранник по вписанной и описанной окружности


