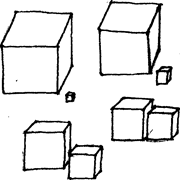
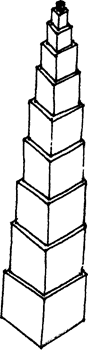
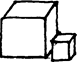
Как работать с материалом. Место для работы — ковер, на котором лежат в беспорядке кубики

Место для работы — ковер, на котором лежат в беспорядке кубики. Ковер должен отличаться по цвету от материала. Учитель берет одной рукой самый большой куб и ставит его перед ребенком, берет следующий по величине куб и ставит точно сверху на первый. Младшие дети берут большой куб обеими руками. Обхватывая и сжимая кубики в руках, дети учатся различать размеры. При этом надо обратить их внимание на равные промежутки между боковыми гранями меньшего и большего кубов и на целенаправленность действий при построении башни. Так, по порядку уменьшения размеров, кубики ставятся друг на друга, и получается башня. Мы можем руками провести по боковым граням башни снизу вверх и сверху вниз. После этого ребенку становится понятной закономерность изменения величин. Башню разбирают кубик за кубиком. Ребенок может повторить упражнение. Этим завершается

весь ход упражнения. Оно закончено, когда материал возвращен на свое место.

Контроль за ошибками:

если заданный порядок построения башни не соблюден, то ошибка определяется зрительно или с помощью рук.

Дальнейшие упражнения:

— вариации основного упражнения в вертикальном и горизонтальном направлениях;

— кубики нужно так поставить друг на друга или положить друг за другом, чтобы угол и две стороны каждого кубика совпали. Самый маленький кубик ставится на образовавшееся свободное место. Самый маленький кубик можно считать воплощенной мерой изменения величин;

— кубики так раскладывают один за другим, чтобы последующий меньший куб приставлялся к середине грани предыдущего поочередно то слева, то справа от ее средней линии. При этом будет понятна статическая закономерность;

— кубики ставятся друг за другом по диагонали;

— изменение заданного порядка 10—1 с учетом гармонии, в вертикальном и горизонтальном направлениях:

10-5-9-4-8-3-7-2-6-1

или

10-1-9-2-8-3-7-4-6-5.

Через подобную закономерность ребенок может найти много вариаций работы с материал

— Ряд кубиков прерывают, вынимая из него один кубик, и ребенку становится очевидной дисгармония.

— Башня строится с закрытыми глазами.

— Комбинационные игры с Коричневой лестницей, Красными штангами, Коричневой лестницей и Красными штангами одновременно.

Словесный урок:

большой — маленький,

большой — больше — самый большой,

маленький — меньше — самый маленький,

самый большой — самый маленький,

больше, чем — меньше, чем.

Этот раздел типичен для всех материалов, где составляются какие-либо ряды.

1-я ступень:

Учитель выбирает из 10 кубиков самый большой и самый маленький. Понятие будет выработано при помощи трехступенчатого урока. Самый поразительный контраст наиболее эффективен. Остальные кубики остаются на своем месте, чтобы внимание ребенка было направлено только на эти два кубика. Учитель берет самый большой куб, обхватывает его говорит: «Из этих двух вот этот большой». Затем он берет самый маленький в руку, показывает его ребенку и говорит: «Из этих двух кубиков вот этот маленький». Так как понятие «большой — маленький» необходимо для дальнейшей работы, продемонстрировав его на других кубиках.

 

2-я ступень:

После того, как на 1-й ступени учитель назвал ребенку сопоставление размеров, он может теперь углубить понятие «большой — маленький». В большинстве случаев переход от 1-й ко 2-й ступени происходит немедленно. Он просит ребенка: «Дай мне из этих двух большой куб! Дай мне маленький кубик!» При этом он пробует использовать возможно большее количество вариаций с другими парами кубиков.

3-я ступень:

Когда ребенок совершенно уверен в выборе куба, можно перейти к 3-й ступени. Теперь ребенок должен быть в состоянии назвать, большим или маленьким является один куб по сравнению с другим. Перед ребенком ставят пару кубиков и спрашивают: «Какой этот куб| Ребенок отвечает: «Большой».—«А этот кубик?»—«Маленький!»

«Большой — больше — самый большой». «Маленький—меньше — самый маленький».

Из 10 кубиков учитель выбирает 3 самых больших (1-я ступень.) Наименьший из них сравнивает с очевидно меньшим четвертым кубом. Показывает на большой куб и говорит:

«Этот большой!» Затем указывает на следующий по величине и говорит: «Этот больше!» Наконец он берег самый большой и говорит: «Из трех этот—самый большой!» Так же прорабатываются понятия «маленький — меньше — самый маленький». 2-я и 3-я ступени урока могут относиться только к предметам, выбранным в порядке увеличения их размеров. Они исходят из основного предмета, в данном случае куба, называемого «большим». Назвать отдельный куб можно, лишь сравнивая друг с другом 3 куба. Учитель просит ребенка расположить кубики по возрастанию или убыванию размеров.

«Самый большой — самый маленький».

При составлении ряда из нескольких кубиков нужно словесно выделить два внешних кубика. «Из кубиков вот этот—самый большой, а этот—самый маленький!» Ребенок выбирает в другом гармонично построенном ряду наибольший и наименьший кубики.

«Больше, чем — меньше, чем».

 

 

В дальнейшем основываются на точном названии величины куба внутри некоторого ряда, например, 10. Учитель берет куб 5 и сопоставляет его с другими кубиками ряда: «Этот меньше, чем те!» При этом он указывает на кубы 6, 7, 8, 9, 10. «Он больше, чем эти!» При этом он показывает на кубы 4, 3, 2, 1.

Применение:

— предложить найти кубы равного размера;

— перенос понятия «большой—маленький» на предметы;

— предложить найти градации величин других предметов.