ПОНЯТИЕ КУБИЧЕСКИХ СПЛАЙНОВ
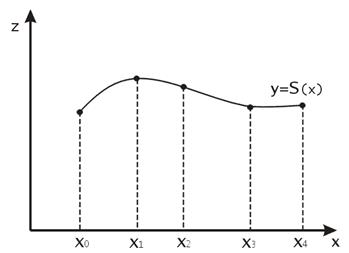
Задача геометрического моделирования сплошных тел является важной областью машинной графики. Анализ состояния современного программного обеспечения убедительно показывает возрастающую роль компьютерной графики. Она выполняет самые разнообразные функции. Здесь и дизайн, привлекающий внимание к программным и информационным продуктам и повышающий комфортность работы в их среде. Здесь и организационная функция, когда графическими средствами распределяется пространство вывода информации, улучшая эргономические характеристики системы. С помощью графических сред программирования и их отдельных элементов существенно изменились временные затраты на создание программных продуктов и сам процесс программирования. Новые разработки аппаратного обеспечения подняли на новый уровень качество изображений как в векторной, так и в растровой графике. Появление новых алгоритмов сжатия растровой информации совместно с увеличением быстродействия процессоров и объема памяти дало мощный толчок распространению видеоинформации. Таким же мощным стимулом развития компьютерной графики явились достижения в области коммуникаций. Все вышесказанное подтверждает необходимость глубоких знаний в области компьютерной графики, как для разработчиков программного обеспечения, так и для пользователей графических систем, где знание основ позволит глубже и быстрее осваивать возможности системы, особенно недокументированные. Для ввода в компьютер растровых и создания векторных изображений и их редактирования разработан широкий спектр программных средств для самых различных групп пользователей. Отметим что, несмотря на огромный выбор, потребность в создании новых программ существует. Все вышесказанное подтверждает актуальность изучения вопросов компьютерной графики. Сплайны - это гладкие (имеющие несколько непрерывных производных) кусочно-полиномиальные функции, которые могут быть использованы для представления функций, заданных большим количеством значений, для которых неприменима аппроксимация одним полиномом. Так как сплайны гладки, экономичны и легки в работе, они используются при построении произвольных функций для: o моделирования кривых; o аппроксимации данных с помощью кривых; o выполнения функциональных аппроксимаций; o решения функциональных уравнений. Рассмотрим задачу проведения гладких кривых по заданным граничным точкам, или задачу интерполяции. Поскольку через две точки можно провести сколь угодно много гладких кривых, то для решения этой задачи необходимо ограничить класс функций, которые будут определять искомую кривую. Математическими сплайнами называют функции, используемые для аппроксимации кривых. Важным их свойством является простота вычислений. На практике часто используют сплайны вида полиномов третьей степени. С их помощью довольно удобно проводить кривые, которые интуитивно соответствуют человеческому субъективному понятию гладкости. Термин “сплайн” происходит от английского spline – что означает гибкую полоску стали, которую применяли чертежники для проведения плавных кривых, например для построения обводов кораблей или самолетов. Рассмотрим в начале сплайновую функцию для построения графика функции одной переменной. Пусть на плоскости задана последовательность точек 1) Функция должна проходить через все точки: 2) Функция должна быть дважды непрерывно дифференцируема, то есть иметь непрерывную вторую производную на всем отрезке На каждом из отрезков
Рис. 20. Сплайновая функция
Задача построения полинома сводится к нахождению коэффициентов с первым условием получаем Перейдем к более сложному случаю – заданию кривых в трехмерном пространстве. В случае функционального задания кривой
Координаты точек на кривой описываются вектором
Одним из способов задания параметрического кубического сплайна является указание координат начальной и конечной точек, а также векторов касательных в них. Такой способ задания называется формой Эрмита. Обозначим концевые точки Будем решать задачу нахождения четверки коэффициентов
Перепишем выражение для
Обозначим вектор строку Из (*) следует, что
Эта система решается относительно
Здесь Выпишем в явном виде формулы для вычисления координат точек сплайна. Так как
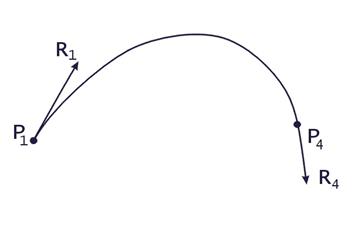
Четыре функции в скобках называются функциями сопряжения. Форму кривой, заданной в форме Эрмита, легко изменять, если учитывать, что направление вектора касательной задает начальное направление, а модуль вектора касательной задает степень вытянутости кривой в направлении этого вектора, как показано на рис. 21.
Рис. 21. Параметрический сплайн в форме Эрмита
Вытянутость кривой вправо обеспечивается тем, что Рассмотрим форму Безье, которая отличается от формы Эрмита способом задания граничных условий, а именно вместо векторов
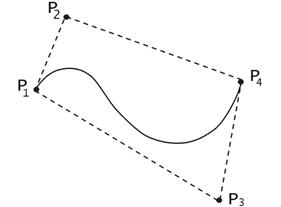
Рис. 22. Параметрический сплайн в форме Безье
Переход от формы Эрмита к форме Безье осуществляется преобразованием
где
Заметим, что матрица вида
|

 ,
, 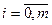 , причем
, причем 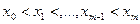 . Определим искомую функцию
. Определим искомую функцию 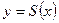 , причем поставим два условия:
, причем поставим два условия: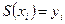 ,
,  .
. ,
, 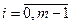 , будем искать нашу функцию в виде полинома третьей степени:
, будем искать нашу функцию в виде полинома третьей степени: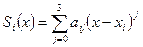 .
.
 . Поскольку для каждого из отрезков
. Поскольку для каждого из отрезков  . Для нахождения всех коэффициентов определим соответствующее количество уравнений. Первые
. Для нахождения всех коэффициентов определим соответствующее количество уравнений. Первые 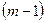 уравнений получаем из условий совпадения значений функции во внутренних узлах
уравнений получаем из условий совпадения значений функции во внутренних узлах  ,
, 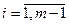 . Следующие
. Следующие  уравнений получаем аналогично из условий совпадения значений первых и вторых производных во внутренних узлах. Вместе
уравнений получаем аналогично из условий совпадения значений первых и вторых производных во внутренних узлах. Вместе уравнений. Недостающие два уравнения можно получить заданием значений первых производных в концевых точках отрезка
уравнений. Недостающие два уравнения можно получить заданием значений первых производных в концевых точках отрезка 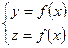 возможны многозначности в случае самопересечений и неудобства при значениях производных равных
возможны многозначности в случае самопересечений и неудобства при значениях производных равных 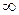 . Ввиду этого будем искать функцию в параметрическом виде. Пусть
. Ввиду этого будем искать функцию в параметрическом виде. Пусть  - независимый параметр, такой что
- независимый параметр, такой что  . Кубическим параметрическим сплайном назовем следующую систему уравнений:
. Кубическим параметрическим сплайном назовем следующую систему уравнений: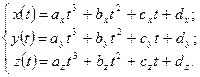
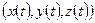 , а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты
, а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты  :
:
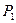 и
и  , а касательные векторы в них
, а касательные векторы в них 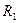 и
и  . Индексы выбраны таким образом с учетом дальнейшего изложения.
. Индексы выбраны таким образом с учетом дальнейшего изложения.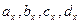 , так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна:
, так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна: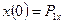 ,
, 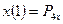 ,
,  ,
, 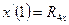 . (*)
. (*)
 .
.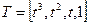 и вектор столбец коэффициентов
и вектор столбец коэффициентов 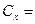
 .
.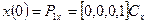 ,
,  . Для касательных
. Для касательных 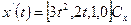 ,
, 
 ,
,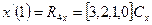 . Отсюда получаем векторно-матричное уравнение:
. Отсюда получаем векторно-матричное уравнение: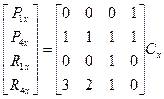 .
.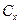 нахождением обратной матрицы размером
нахождением обратной матрицы размером  .
. .
.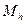 - эрмитова матрица,
- эрмитова матрица,  - геометрический вектор Эрмита. Подставим выражение
- геометрический вектор Эрмита. Подставим выражение 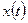 :
:  . Аналогично для остальных координат:
. Аналогично для остальных координат:  ,
,  .
.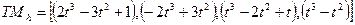 , то, умножая справа на
, то, умножая справа на 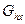 , получаем
, получаем
 .
.
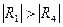 .
. и
и  , как показано на рис. 5, такие, что выполняются условия:
, как показано на рис. 5, такие, что выполняются условия:  и
и  .
.
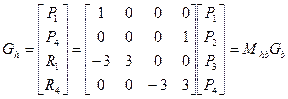 , (*)
, (*)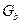 - геометрический вектор Безье. Подставляя это в выражение для
- геометрический вектор Безье. Подставляя это в выражение для 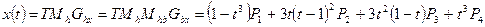 Полезным свойством сплайнов в форме Безье является то, что кривая всегда лежит внутри выпуклой оболочки, образованной четырехугольником
Полезным свойством сплайнов в форме Безье является то, что кривая всегда лежит внутри выпуклой оболочки, образованной четырехугольником 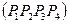 . Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице.
. Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице. - называется матрицей Безье.
- называется матрицей Безье.


