НЕРАВНОМЕРНАЯ СЕТКА. ИЗОЛИНИИ
Неравномерной сеткой назовем модель описания поверхности в виде множества отдельных точек {(х0, yQ, z0), (x1, y1, z1),..., (хп-1 уn-1, zn-1.,)}, принадлежащих поверхности. Эти точки могут быть получены, например, в результате измерений поверхности какого-нибудь объекта с помощью определенного оборудования. Такую модель можно считать обобщением для некоторых рассмотренных нами моделей. Например, векторная полигональная модель и равномерная сетка могут считаться разновидностями неравномерной сетки. Эти разновидности мы рассмотрели в отдельности, так как они играют важную роль для решения задач КГ. А вообще, может существовать много вариантов классификации способов описания поверхностей. Следует учитывать определенную условность нашего перечня моделей поверхностей, последовательность перечисления таких моделей может быть и другой. Рассмотрим модель поверхности в виде множества точечных значений, логически никак не связанных между собой. Неравномерность задания опорных точек усложняет определение координат для других точек поверхности, которые не совпадают с опорными точками. Нужны специальные методы пространственной интерполяции. Так, например, можно поставить такую задачу — по известным координатам (jc, у) вычислить значения координаты z. Для этого необходимо найти несколько самых близких точек, а потом вычислить искомое значение z, исходя из взаимного расположения этих точек в проекции (х, у). Как мы уже рассмотрели выше, для равномерной сетки это намного проще — поиска фактически нет, мы сразу рассчитываем индексы самых близких опорных точек. Еще одна задача — отобразить поверхность. Эту задачу можно решать несколькими способами, в том числе триангуляцией. Процесс триангуляции можно представить себе так (рис. 17). Сначала находим первые три самые близкие друг другу точки — и получаем одну плоскую треугольную грань. Потом находим точку, ближайшую к этой грани, и образовываем смежную грань. И так далее, пока не останется ни одной отдельной точки. Это общая схема, в литературе описано много разных способов триангуляции. Довольно часты ссылки на триангуляцию Делоне.
Рис. 17. Триангуляция неравномерной сетки
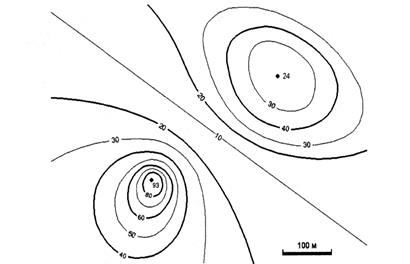
Описание поверхности треугольными гранями можно уже считать разновидностью векторной полигональной модели. В англоязычной литературе для нее встречается такое название: TIN (Triangulated Irregular Network). После триангуляции получаем полигональную поверхность, отображение которой сделать уже достаточно просто. Рассмотрим еще один из вариантов описания поверхности — изолинии высоты. Любая изолиния состоит из точек, представляющих одно числовое значение какого-то показателя, в данном случае — значение высоты (рис. 18, 19). Изолинии высоты также можно вообразить себе как контуры разреза поверхности горизонтальными плоскостями (поэтому для изолиний высоты часто применяется название "горизонтали"). Описание поверхности изолиниями высоты часто используется, например, в картографии. По бумажной карте можно с определенной точностью рассчитать высоты в точках местности, углы наклона и прочие параметры рельефа. Необходимо заметить, что описание рельефа земной поверхности изолиниями высоты неправильно представлять как разрезы горизонтальными плоскостями, ибо поверхность Земли не плоская. Если бы Земля была шаром, то изолинии высоты можно было бы трактовать как изолинии радиусов. Однако Земля — это не шар, она имеет намного более сложную форму, названную геоидом. В геодезии и картографии геоид аппроксимируют с определенной точностью разнообразными эллипсоидами. Таким образом, здесь можно говорить об изолиниях некоторых условных высот в специальных системах координат. Конечно, для описания поверхности можно использовать не только изолинии высоты, но и другие изолинии, например
Рис.19. Та же поверхность в аксонометрической проекции
В компьютерных системах изолинии часто описываются векторно — полилиниями. Используются также изолинии в виде сплайновых кривых. Точки, которые составляют изолинии, и отдельные опорные точки располагаются неравномерно. Это усложняет расчет координат точек поверхности. В графических компьютерных системах для выполнения многих операций и в первую очередь — для показа поверхности обычно необходимо преобразовывать описание поверхности в другую форму. Преобразование изолиний в полигональную модель также выполняется методами триангуляции (здесь алгоритмы триангуляции сложнее, чем для триангуляции отдельных точек). Для преобразования неравномерной сетки в равномерную используют специальную интерполяцию. Положительные черты неравномерной сетки: использование отдельных опорных точек, наиболее важных для заданной формы поверхности, обусловливает меньший объем информации по сравнению с другими моделями, например с равномерной сеткой; наглядность показа рельефа поверхности изолиниями на картах, планах. Недостатки: невозможность или сложность выполнения многих операций над поверхностями; сложные алгоритмы преобразования в другие формы описания поверхностей.
|