СИНТЕЗ ТВЕРДОГО ТЕЛА ПО ПРОЦЕДУРНОМУ ОПИСАНИЮ

 

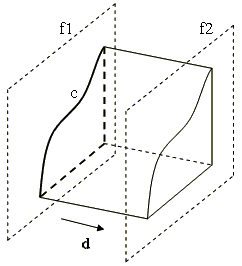
В современных системах геометрического моделирования сформировались следующие способы синтеза твердотельных моделей:

· за основу берется конкретный примитив (параллелепипед, цилиндр, шар);

· из других твердотельных моделей (операции булевых сочетаний, модификация граней, фаски) и их частей (выдавливание, вращение грани);

· из кривых с помощью процедурных методов.

В данной работе имеет смысл использовать только последний способ. Наиболее распространенными процедурными методами синтеза являются:

· выдавливание плоской кривой по направлению;

· вращение плоской кривой вокруг оси;

· лофтинг интерполяция поверхности между плоскими замкнутыми кривыми (профили, сечения, образующие);

· протягивание плоской кривой (профиль, или образующая) вдоль плоской или пространственной кривой (путь, или направляющая).

Рассмотрим принципы синтез твердотельных моделей на примере двух первых, наиболее простых методах.

В каждом случае на кривые, участвующие в синтезе, налагаются определенные ограничения во избежание получения топологически некорректных многосложных моделей.

Тело выдавливания, как видно из рис. 9, образуется из двух усеченных плоских патчей (f₁ и f₂) и неусеченных патчей, составляющих боковую поверхность тела. Отсюда очевидны два необходимых условия:

· образующий контур c (цепочка кривых) не должен иметь самопересечений;

· образующий контур должен быть замкнут;

· направление выдавливания d не должно быть параллельно плоскости образующего контура c.

Рис. 9. Тело выдавливания

 

Тело вращения можно построить двумя способами: путем полного обращения образующей вокруг оси (рис. 10, а) и неполного обращения (рис. 10, б). В первом случае боковая поверхность может быть представлена с помощью одного полного (неусеченного) патча и двух (верхний и нижний) усеченных патчей. Во втором случае добавляется еще два усеченных патча f3 и f4.

Рис. 10. Тела вращения: а – полный оборот, б – неполный оборот

 

Поскольку при построении будут получены конические кривые (с1) и поверхности (f2), то в целях точности целесообразно их построения осуществлять по специальным алгоритмам с использованием весов NURBS.

Для соблюдения правильности топологии должны выполняться следующие условия:

- образующая не должна пересекать ось вращения;

- образующая не должна пересекать саму себя.

Пример использования произвольной параметрической поверхности для построения твердотельной модели проиллюстрирован на рис. 11.

Рис. 11. Твердое тело как параллелепипед, ограниченный параметрической поверхностью

 

Здесь твердотельная модель состоит из:

1. неусеченной поверхности f1 как NURBS-аппроксимация графика функции двух переменных;

2. плоской прямоугольной неусеченной грани f2;

3. четырех боковых неусеченных граней f3-f6.