Однофакторный корреляционный и регрессионный анализ

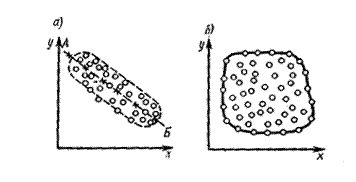
Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи.

Задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y = f(x), которая наилучшим образом описывает имеющиеся экспериментальные данные.

Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.

Корреляционное поле и корреляционная таблица являются исходными данными при корреляционном анализе. По тесноте группирования точек вокруг прямой или кривой линии, по наклону линии можно визуально судить о наличии корреляционной связи. Так, из рис. 1 (а)видно, что экс­периментальные данные имеют определенную связь меж­ду х и у, а измерения, приведенные на рис. 1 (б), такой связи не показывают. Корреляционное поле характеризует вид связи между х и у.

Рис. 1. Корреляционное поле

Для у в литературе можно встретить следующие названия: функция отклика, зависимая переменная; х называют входной переменной, независимой переменной, фактором, регрессором.

По форме поля можно ориентировочно судить о форме графика, характеризующего прямолинейную или криволинейную зависимости. Даже для вполне выражен­ной формы корреляционного поля вследствие статистиче­ского характера связи исследуемого явления одно значе­ние х может иметь несколько значений у. Если на корре­ляционном поле усреднить точки, т.е. для каждого значения x_i, определить и соединить точки , то можно будет получить ломаную линию, называемую экспериментальной регрессионной зависимостью (линией). На­личие ломаной линии объясняется погрешностями изме­рений, недостаточным количеством измерений, физичес­кой сущностью исследуемого явления и др. Если на корреля­ционном поле провести плавную линию между , которая равноудалена от них, то получится новая теорети­ческая регрессионная зависимость - линия АБ (рис. 1, а).

Различают однофакторные (парные) и многофактор­ные регрессионные зависимости. Однофакторная регрессия при парной зависимости может быть аппроксимирована прямой линией, параболой, гиперболой, логарифмичес­кой, степенной или показательной функцией, полиномом и др. Двухфакторное поле можно аппроксимировать пло­скостью, параболоидом второго порядка, гиперболои­дом. Для переменных факторов связь может быть уста­новлена с помощью n-мерного пространства уравнения­ми второго порядка.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типов функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически – перебором и оценкой функций разных типов и т.п. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчётов преобразуют (путём логарифмирования или замены переменных) в линейную форму.