Корреляционный анализ.
Для определения коэффициента корреляции строим статистическую таблицу.
(2)
Таблица 2 Статистическая таблица
После подстановки в формулу получим r=0,57 – связь положительная и достаточно тесная. 3. Регрессионный анализ. На корреляционное поле наносим результаты эксперимента и визуально определяем вид зависимости.
Рис. 3. Корреляционное поле По рис. 3 определяем, что полученные точки можно аппроксимировать прямой линией. Таким образом, для описания полученных точек можно использовать линейную регрессию: y = b0 + b1x, в которой неизвестны коэффициенты регрессии b0 и b1
= 3,64 (3)
= 0,07 (4)
Полученное уравнение регрессии, которое определяет аппроксимирующую линейную функцию для исходных данных, представляет собой:
4. Определяется значимость по критериям Стьюдента и Фишера. Значимость коэффициента корреляции определяем с помощью критерия Стьюдента:
где r – коэффициент корреляции; n – количество измерений. Сравним полученное значение с табличным значением критических точек распределения Стьюдента (по табл. П4 [7]). Для уровня значимости р=0,05 и числа степеней свободы к=n - 2=4 определяем tкр(0,05; 4). Проверяем, если tф > tкр, то найденный коэффициент корреляции значимо оценивает связь между переменными х и у. В нашем примере tф = 3,04 > tкр = 2,13. В обратном случае нулевую гипотезу про равенство нулю генерального коэффициента корреляции не отклоняют; таким образом, х и у не коррелируют между собой Определим значимость уравнения регрессии, используя критерий Фишера. Данные для расчета остаточной дисперсии заносим в таблицу 3. Общая дисперсия:
Остаточная дисперсия:
Таблица 3
|



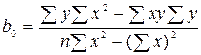
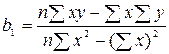
 =3,64 + 0,07х (5)
=3,64 + 0,07х (5)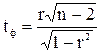 , (6)
, (6)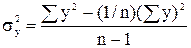 =0,13 (7)
=0,13 (7) = 0,047 (8)
= 0,047 (8)


