Подвижные сосредоточенные источлнки
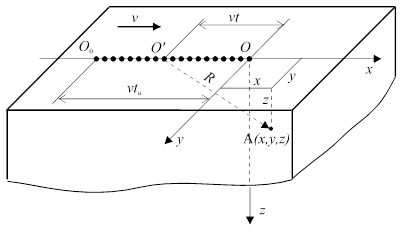
а ) Подвижный точечный источник на поверхности полубесконечного тела. По поверхности полубесконечного тела с постоянной скоростью v движется точечный источник теплоты постоянной мощности q (рис. 22). Источник перемещается из точки О 0 направлении оси х. Температурное поле подвижного источника записывают в подвижной системе координат, начало которой совмещают с источником теплоты.
Рис. 22. К выводу уравнения температурного поля подвижного точечного источника на поверхности полубесконечного тела.
Для определения температурного поля используют метод источников. Для этого все время tн действия источника разбивают на бесконечно малые элементы. Температуру в любой точке тела представляют суммой приращений температуры при распространении теплоты от отдельных мгновенных точечных источников с учетом времени и места их приложения. Например, приращение температуры в точке А (х, у, г) от мгновенного точечного источника теплоты, который действовал в течение времени dt в точке О', равно:
Температурное поле подвижного точечного источника определяют путем суммирования приращений температуры от бесконечного числа мгновенных точечных источников, распределенных по отрезку O 0 O и в интервале времени от 0 до tн:
После преобразований:
где R 2= x 2+ y 2+ z 2. Характерной особенностью температурного поля подвижного источника является то, что нагретая зона в подвижной системе координат, связанной с источником, непрерывно увеличивается во времени, стремясь к некоторому предельному состоянию. Поэтому процесс нагрева подразделяют на два периода: 1) теплонасыщение, когда размеры связанной с источником нагретой зоны увеличиваются; 2) предельное состояние, когда вместе с источником перемещается неизменяющееся температурное поле, которое называют квазистационаным. Уравнение предельного состояния подвижного точечного источника можно получить из уравнения (67), принимая t н = ¥. Оно имеет вид:
Рассмотрим частный случай — температурное поле предельного состояния неподвижного непрерывно действующего точечного источника. Подставляя v =0 в уравнение (68), получим уравнение стационарного температурного поля:
Поле симметрично относительно точки О. Изотермические поверхности - концентрические полусферы. Температура в направлении от источника теплоты убывает обратно пропорционально радиусу-вектору R. Температура на данном расстоянии R прямо пропорциональна мощности источника q и обратно пропорциональна коэффициенту теплопроводности l.
Рис. 23. Температурное поле предельного состояния при движении точечного источника теплоты по поверхности полубесконечного тела (q =4000 Вт; v= 0,1 см/с; а =0,1 см2/с; l=0,4 Вт/см×K): а - схема расположения координатных осей; б - изотермы на поверхности хОу; в - распределение температуры по прямым, параллельнымоси х и расположенным на поверхности тела; г - распределение температуры по прямым, параллельным оси у и лежащим в поперечной плоскости уОг; д - изотермы в поперечной плоскости у0z, проходящей через центр источника теплоты.
Температурное поле (68) предельного состояния подвижного источника симметрично относительно оси Ох (рис. 23). Изотермы на поверхности хОу представляют собой овальные кривые, смещенные относительно источника в сторону, обратную направлению его перемещения. Они сгущены впереди источника и разрежены позади него. Уравнение распределения температуры по оси Ох перед источником получаем из уравнения (68) подстановкой х=R:
Множитель ехр(-vR/a) всегда меньше единицы. Поэтому чем больше скорость v и меньше коэффициент температуропроводности а, тем быстрее убывает температура впереди источника. Распределение температуры по оси Ох позади источника (x=-R) выражается уравнением:
Таким образом, распределение температуры на отрицательной полуоси x <0 не зависит от скорости перемещения точечного источника. Распределение температуры по оси Оу получим, полагая в уравнении (68) x =0:
Следовательно, в боковом направлении изотермы также сгущены, но в меньшей степени, чем перед источником, т. к. exp(- vR /2 a)>exp(- vR/a). Степень вытянутости температурного поля зависит от параметра vR/a. В области малых значений vR/a изотермы близки к окружностям, при больших значениях vR/a они вытянуты вдоль оси Ох. Изотермические поверхности являются поверхностями вращения относительно оси Ox. Пунктирной линией на рис. 23 соединены точки с максимальной температурой на плоскости хОу. Поверхность вращения этой линии вокруг оси Ох разделяет тело на две области: впереди нее тело нагревается, позади - остывает. б) Подвижный линейный источник в пластине. Линейный источник теплоты мощностью q перемещается в направлении оси х. Мощность источника равномерно распределена по толщине d пластины. Уравнение температурного поля выводится в данном случае аналогично уравнению для подвижного точечного источника. Нагрев пластины подвижным линейным источником также разделяют на периоды теплонасыщения и предельного состояния. Уравнение температурного поля предельного состояния в подвижной системе координат с учетом поверхностной теплоотдачи имеет вид:
где K 0 (u) - функция Бесселя от мнимого аргумента второго рода нулевого порядка. Температура по толщине пластины не меняется. Следовательно, изотермические поверхности в пластине представляют собой цилиндрические поверхности. Качественно распределение температуры на поверхности пластины аналогично распределению температуры на поверхности полубесконечного тела. Однако, изотермы на поверхности пластины еще более вытянуты в направлении, обратном направлению движения источника, и очерчивают области большие по величине, чем соответст вующие изотермы на поверхности полубесконечного тела. Раcпределение температуры в пластине по отрицательной полуоси x <o в отличие от распределения в полубесконечном теле зависиг от скорости движения источника. Рассмотрим влияние мощности q и скорости v источника на температурное поле предельного состояния. С увеличением скорости v при q =const области, нагретые выше определенной температуры, уменьшаются по площади, а соответствующие изотермы уменьшаются по длине и ширине и сгущаются перед источником. С увеличением мощности q при v =const области, нагретые выше определенной температуры, увеличиваются по площади, причем их размеры растут не пропорционально увеличению мощности, а более интенсивно. Увеличение длины изотермы происходит быстрее, чем ширины. Одновременное увеличение мощности и скорости источника при постоянной погонной энергии q/v приводит к увеличению длины изотерм. Ширина изотерм также увеличивается, но стремится к определенному значению. Размеры площадей, ограниченных изотермами, приближенно прямопропорциональны мощности источника.
Рис. 24. Влияние теплофизических свойств металла на характер температурного поля в плавстине (q = 4200 Вт; v = 0,2 см/с; d = 1 см).
Большое влияние на температурное поле предельного состояния оказывают теплофизические свойства металла. При уменьшении коэффициента теплопроводности l области, ограниченные изотермами, увеличиваются. Длина изотерм увеличивается в большей степени, чем их ширина. Например, область, ограниченная изотермой T =600 °С (рис. 24), в хромоникелевой стали имеет из-за меньшей ее теплопроводности большие размеры, чем в низкоуглеродистой стали. Поэтому одинаковое тепловое воздействие на свариваемый металл при сварке аустенитной стали осуществляется при меньшей погонной энергии, чем при cварке низкоуглеродйстой стали. При сварке алюминия и меди размеры областей, нагретых до высокой температуры, значительно меньше, чем в стали. Благодаря высокой теплопроводности алюминия и меди изотермы в области высоких температур близки к окружностям и меньше сгущены перед источником. Увеличение теплоемкости металла оказывает примерно такое же влияние, как увеличение скорости при постоянной мощности источника, - области, нагретые выше определенной температуры, уменьшаются, изотермы укорачиваются и сужаются. Рассмотрим частный случай - температурное поле предельного состояния неподвижного непрерывно действующего линейного источника в пластине. Полагая в уравнении (69) v= 0, получим уравнение стационарного температурного поля:
Температурное поле (70) является осесимметричным. Изотермические поверхности - круглые цилиндры с осью, совпадающей с линейным источником теплоты. Следует заметить, что стационарное температурное поле в пластине достигается лишь при наличии теплоотдачи в окружающую среду. Если теплоотдача отсутствует, то нагретая зона непрерывно расширяется. Действительно, при b =0 в) Подвижный плоский источник теплоты в стержне. Плоский источник теплоты постоянной мощности q перемещается с постоянной скоростью v в направлении оси х вдоль стержня. Теплота источника равномерно распределена по поперечному сечению F стержня. Уравнение температурного поля предельного состояния в подвижной системе координат с учетом поверхностной теплоотдачи имеет вид:
Температурное поле характеризуется быстрым нарастанием температуры перед источником и плавным спадом температуры позади него. Крутизна поля перед источником возрасгает с увеличением скорости и уменьшением коэффициента температуропроводности а. В частном случае, когда v =0, температурное поле неподвижного непрерывно действующего плоского источника теплоты в стержне описывается уравнением:
Стационарное температурное поле в стержне достигается лишь при наличии теплоотдачи в окружающую среду.
|

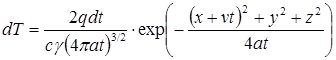 . (66)
. (66) .
.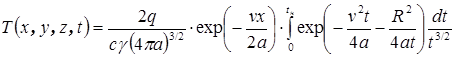 , (67)
, (67) . (68)
. (68)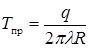

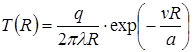 .
.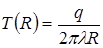 .
.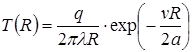 .
. , (69)
, (69)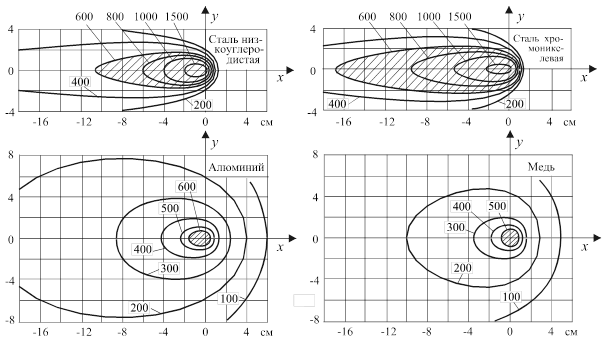
 . (70)
. (70)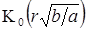 стремится к бесконечности и температура Т пр возрастает беспредельно.
стремится к бесконечности и температура Т пр возрастает беспредельно. . (71)
. (71) .
.


